1 Modelación del Mundo Real
1.1 Conceptos Espaciales
1.1.1 Espacio absoluto vs Espacio Relativo
En diferentes idiomas, el término espacio tal como lo usamos para referirnos al espacio geográfico tiene significados distintos. En inglés, la connotación principal del espacio está conectada con el “espacio exterior”: un vasto vacío, tal vez infinito, en el que hay cuerpos celestes como soles, planetas, lunas y asteroides. Por el contrario, el término correspondiente en el idioma alemán “Raum” se refiere a una escala completamente diferente. Se refiere a una “habitación” en una casa, que es un contenedor espacial claramente confinado que per se está vacío (Figura 1.1).
La noción de “espacio geográfico” se refiere a escalas entre el alemán “Raum” y la noción inglesa de “espacio exterior”. Sin embargo, ambos términos se encuentran en la misma tradición de pensar en el espacio como un contenedor métrico y vacío que está lleno de objetos. Newton llamó a esta conceptualización del espacio “espacio absoluto”.

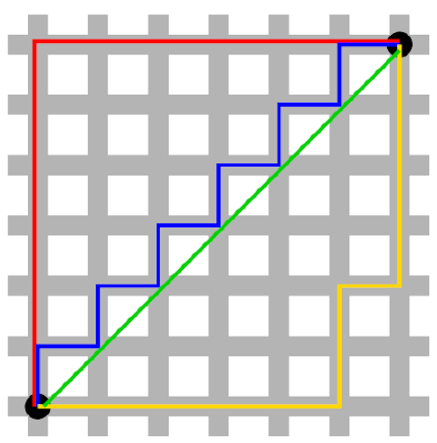
La formulación matemática de cómo las distancias y direcciones en el espacio absoluto se pueden medir cuantitativamente, se remonta a los antiguos griegos, más específicamente: a Euclides. El espacio métrico homogéneo, que subyace a un SIG, se denomina a menudo espacio euclidiano. Otra métrica que comúnmente subyace en el espacio absoluto es el espacio de Manhattan, que se utiliza para entornos cuadriculados donde las mediciones de distancia siguen líneas centrales de cuadrícula (Figura 1.2). El marco de referencia para el espacio geográfico absoluto es, el sistema de coordenadas cartesianas en el que un objeto puede ubicarse sin ambigüedades dentro de ejes ortogonales tridimensionales.
Leibniz, contemporáneo de Newton, sugirió otra forma de pensar sobre el espacio, que denominó espacio relativo. El concepto subyacente es que no puede haber nada como el espacio vacío. La dimensión espacial emerge de las relaciones entre los objetos. Si no hubiera objetos, no quedaría ningún espacio vacío, simplemente no habría nada. Por lo tanto, el espacio relativo no depende de ningún sistema de coordenadas como marco de referencia externo.
Las relaciones que se pueden establecer entre los objetos, a través de la clave de ubicación (en el espacio absoluto) permiten relacionar cosas a través de escalas y temas específicos. Estos lazos entre los objetos vecinos y su entorno local no contradicen su localización respectiva en el espacio absoluto. Sin embargo, esta localización relativa proporciona una comprensión más profunda de sus propiedades espaciales. El análisis de las relaciones espaciales relativas, es lo que hace que el análisis geoespacial sea tan poderoso: si solo tuviéramos una fila de automóviles, esto no tendría sentido. Sin embargo, si conectamos estos automóviles a través de su ubicación relativa en una red de calles, podemos comenzar a analizar los patrones de tráfico.
Para quienes deseen leer más sobre conceptualizaciones del espacio, se recomienda las publicaciones de Space, time, geography de Couclelis (1999) y Models in Geography por Mazúr y Urbánek (1983).
1.1.2 Campos y objetos
Independientemente, del debate del espacio absoluto versus el relativo, en última instancia nos enfocaremos en las cosas en sí.
Hay dos posibilidades de cómo podemos pensar sobre las entidades en el espacio geográfico: ya sea como campos continuos o como objetos discretos. Si bien vemos la topografía, ¡ojo! No topología general de un paisaje, como una superficie continua, podemos identificar pueblos individuales, ríos o campos de maíz dentro de ese paisaje. En la vista de objetos identificamos objetos discretos con límites nítidos: casas, calles, ríos y montañas. Esta es la visión predominante, cuando pensamos en el mundo. En un primer paso identificamos el objeto, luego lo llenamos con atributos y lo ubicamos. Dentro de su extensión, un objeto es homogéneo; sus atributos no varían dentro del objeto. La geometría euclidiana describe las cuatro categorías de objetos espaciales: puntos, líneas, polígonos y sólidos.
Distinguimos entre objetos de facto e intangibles (fiat). Los objetos de facto son entidades físicas tangibles con límites que pueden detectarse directamente, como una casa o un lago. Los objetos intangibles en contraste son inmateriales. Ellos son creados por convenciones sociales, como distritos electorales o propiedad de la tierra. La vista de campo es la conceptualización complementaria de entidades espaciales, en la que la variación de un atributo se percibe en el espacio. Ejemplos típicos serían la temperatura prevista de Europa en el pronóstico del tiempo, o la elevación de las colinas ondulantes a nuestro alrededor como se ve desde la cima de una colina. Los atributos “temperatura” o “elevación” se pueden medir y mapear en cualquier punto dentro del área de interés. El cambio en el espacio es continuo y puede ser expresado en una función matemática o como un campo de valores.
1.1.3 Relaciones espaciales
Una vez definido el contexto (espacio) y las entidades (objetos y campos), ahora analizaremos la conceptualización de las relaciones espaciales. La geometría cuantifica las propiedades y relaciones métricas en el espacio absoluto, mientras que la topología describe las relaciones en el espacio relativo.
Geometría
Las propiedades geométricas son longitud (líneas), área (polígonos) y volumen (sólidos), mientras que las relaciones geométricas son por ejemplo: distancia y dirección entre objetos. Las variables geométricas dependen del sistema de coordenadas elegido. Si los datos espaciales se transforman de un sistema de coordenadas a otro, los valores cambian.
Distancia
El cálculo de la distancia es probablemente el algoritmo aplicado con mayor frecuencia en el análisis espacial. Las preguntas típicas son:
- ¿A qué distancia está el supermercado más cercano?
- ¿Cuántos edificios hay dentro de un búfer de 50 m de la carretera?
- ¿Cuál es la distancia de vuelo diario de una ave migratoria en promedio?
Para calcular la distancia entre dos puntos, simplemente podemos usar el teorema de Pitágoras:
\[Distancia_{ab}=\sqrt{\left(X_b-X_a\right)^2+\left(Y_b-Y_a\right)^2}\]
Este cálculo de distancia supone un espacio bidimensional homogéneo. Esta suposición a menudo no es apropiada:
Si las distancias recorridas no son directas (“en línea recta”), sino que están vinculadas a una red. En este caso, se debe sumar la longitud de todos los segmentos de línea recorridos.
Los cálculos de distancia a escalas continentales o globales deben considerar la curvatura de la Tierra. Los diferentes sistemas de referencia de coordenadas realizan trabajos satisfactorios o insatisfactorios para representar con precisión distancias esféricas.
Las distancias espaciales a veces no se aproximan correctamente al tiempo y al esfuerzo invertido para mover esa distancia. Para tener en cuenta dicha distorsión, se pueden aplicar diferentes pesos de distancia a los segmentos de la calle.
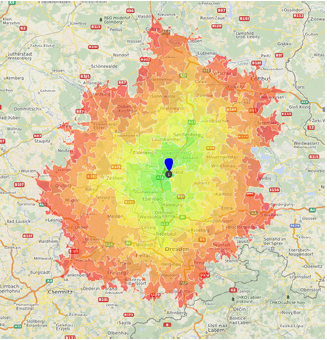
En la Figura 1.3, puede ver categorías de tiempos de viaje vinculados a la red. Cada categoría equivale a 8 minutos de viaje. Mientras que esperaríamos amortiguar de forma circular para las distancias euclidianas, ahora obtenemos líneas distorsionadas de tiempos de viaje iguales, también conocidos como “isócronas”.
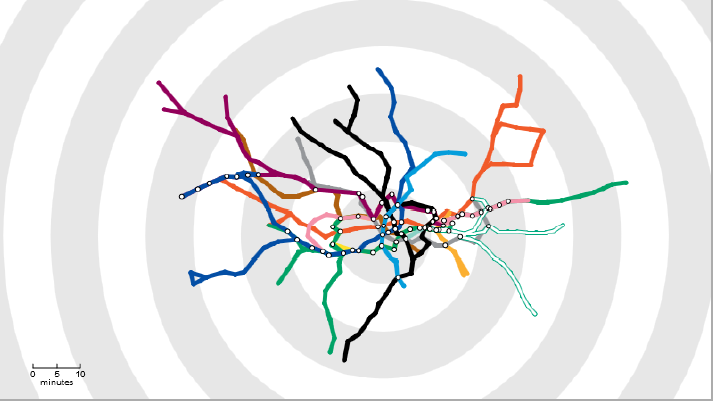
El tiempo de viaje (Travel Time Tube; Figura 1.4) de Londres lleva el principio de las isócronas (más conocido en SIG como Isochrones) a sus extremos: distorsiona el espacio para adaptarse a las isócronas. ¡Échale un vistazo! (Revisa el material adicional para saber más sobre éste tema).
Topología
La topología es la descripción formal de las propiedades espaciales que se conservan bajo deformación continua.
Esto significa que la topología estudia la configuración relativa de los objetos entre sí. A diferencia de la geometría, la ubicación de los objetos en el espacio absoluto es irrelevante en la topología. En la Figura 1.5, hay un globo que está distorsionado de diferentes maneras. Las propiedades geométricas del rectángulo y el punto cambian con la distorsión: el área se contrae o se agranda, la forma se sesga, la distancia y la dirección desde las esquinas del rectángulo hasta el punto central se modifican. Sin embargo, la relación topológica es constante: el punto siempre permanece dentro del polígono.

Las relaciones no solo se pueden definir horizontalmente, sino también jerárquicamente a través de escalas. La definición de relaciones jerárquicas nos permite analizar datos sobre múltiples escalas espaciales y temporales. Considere por ejemplo, viajar a través de largas distancias: comienza conduciendo su camino de acceso privado, gira e ingresa en la carretera del distrito, después la carretera estatal y finalmente la autopista. Acercándose a su destino, sale de la autopista y navega por vías secundarias y terciarias nuevamente hasta llegar a su destino final. Mientras conduce, conecta de forma natural las escalas locales con las nacionales sin tener en cuenta toda la red nacional de carreteras terciarias (Figura 1.6).

Visión funcional sobre relaciones espaciales
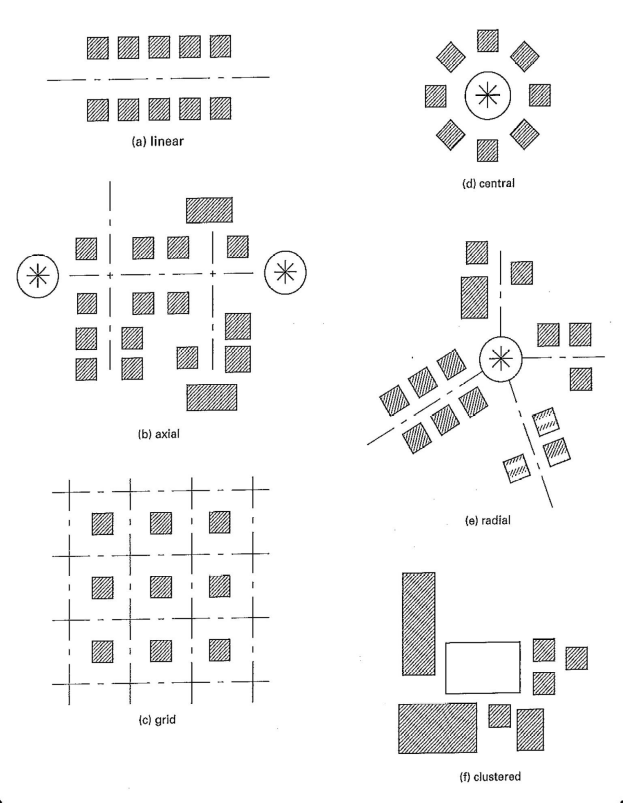
Podemos diseñar la disposición de los objetos para crear relaciones espaciales que permitan funciones específicas. Este es un principio fundamental en la planificación espacial y la arquitectura del paisaje. Considere, por ejemplo, la disposición de casas y calles en la Figura 1.7. ¿Te imaginas cuántas interacciones humanas sucederán en estos lugares? ¿Dónde preferirías vivir?
Del mismo modo, la disposición espacial en un paisaje ofrece hábitats más o menos adecuados para los animales. Desde la perspectiva de una ardilla, es importante que los árboles estén lo suficientemente cerca como para saltar de uno a otro. A un pájaro en contraste, le conviene las brechas entre los árboles como zonas de alimentación. Un ingeniero forestal quiere que los árboles se mantengan cerca para maximizar la cosecha y un inversor puede querer cortar los árboles por completo para construir un supermercado.
Cuando se utiliza SIG en los procesos de toma de decisiones para encontrar una configuración espacial que garantice buenas relaciones funcionales, es importante incluir todos los aspectos relevantes para optimizar la solución general. En este proceso de optimización, los SIG pueden proporcionar información sobre el impacto relativo de un determinado escenario en varios aspectos: mejor accesibilidad a la infraestructura, volumen de tráfico, pérdida de paisaje o fragmentación. Sin embargo, los SIG no pueden proporcionar la “respuesta óptima”. Esto depende de la ponderación de los aspectos individuales de acuerdo con los valores sociales acordados.
Las decisiones permanecen bajo la responsabilidad de los humanos. Los SIG solo pueden apoyar el proceso de toma de decisiones cuantificando relaciones espaciales favorables y no deseadas (y, por lo tanto, funcionales) en escenarios alternativos.
1.1.4 Mapas mentales
En nuestras rutinas diarias percibimos continuamente el espacio, los objetos espaciales y las relaciones espaciales. A partir de esto, construimos mapas en nuestro cerebro, en los que podemos navegar mentalmente: los llamados mapas mentales. Estos proporcionan nuestro marco espacial individual en el que almacenamos y organizamos nuestros recuerdos. Se revisa amplia y constantemente a medida que hacemos nuevas experiencias.
Cuando necesitamos tomar una decisión espacial, por ejemplo, qué ruta tomar para llegar a un punto de encuentro en nuestra ciudad de origen, no nos molestamos en mirar un mapa. Nos referiremos a nuestro mapa mental. A veces nuestro mapa nos engañará y descubriremos que nuestra ruta no era el camino más corto, o que el aeropuerto tarda mucho más de lo esperado.
Para el uso en un SIG, un mapa mental sería bastante inútil. Su sistema de coordenadas está incompleto y distorsionado.
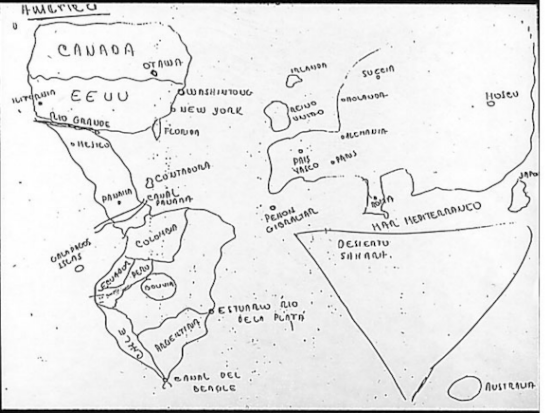
Sin embargo, es importante comprender los mapas mentales de las personas, por ejemplo, con fines de planificación espacial: es importante qué tan accesible o habitable es un área percibida por un ciudadano, y no cómo sugieren algunos indicadores calculados. La Figura 1.8 es más precisa en algunas partes del mundo y muy general en otras. ¿Dónde crees que vive el creador de este mapa?
1.2 Modelando el Mundo Real
Un modelo es una representación abstracta de un sistema, que se crea para un propósito específico.
Un modelo puede ser un modelo físico, una ecuación matemática, un dibujo pintoresco o un diagrama de flujo. Sin embargo, en geoinformática nos interesan los modelos de datos espaciales, es decir, modelos digitales que representan una parte del mundo real de forma espacialmente explícita.
En la década de 1960, antes de la era de los Sistemas de Información Geográfica, Chorley y Haggett (1967) describieron la esencia de un modelo en geografía:
Un modelo puede diseñarse en forma de “…ya sea una teoría, una ley, una hipótesis o una idea estructurada. Puede ser un rol, una relación o una ecuación. Puede ser una síntesis de datos. Lo más importante, desde el punto de vista geográfico, también puede incluir el razonamiento sobre el mundo real por medio de traducciones en el espacio (para dar modelos espaciales) o en el tiempo (para dar modelos históricos)” (Chorley y Haggett 1967 pp 21-22).
El objetivo final de un modelo en geoinformática es representar o tomar “gemelos digitales” de nuestro mundo físico tangible para hacer uso de computadoras para razonar sobre él. Sin embargo, para hacerlo, primero debemos crear estos “gemelos digitales”. Este proceso, en pocas palabras, es el modelado de datos. El modelado de datos no es en absoluto una tarea trivial. Es un proceso de abstracción paso a paso que se basa en los conceptos y métodos de análisis y modelado de sistemas.
1.2.1 El Mapa Como Modelo
Un mapa de papel es una representación abstracta de una parte específica del mundo. Hay mapas en papel para conductores de automóviles, para excursionistas y para turistas. Un mapa cumple todos los criterios de un modelo:
Abstracción
Los modelos no son copias en miniatura de lo real, pero omiten deliberadamente información y reducen el nivel de detalle. El poder de un modelo reside en su abstracción. Sólo se presenta el contenido importante.
Representación
Los modelos son los ‘gemelos virtuales’ de lo real. Se relacionan con objetos y procesos del mundo real. Los modelos espaciales toman las coordenadas geográficas como clave de referencia.
Propósito
Los modelos se crean para un propósito específico. No hay modelos generales, como tampoco hay un mapa general. El proceso de abstracción y generalización está guiado por el propósito. Por lo tanto, un modelo nunca puede ser verdadero o correcto, sino sólo adecuado (válido) para un propósito específico.
1.2.2 Modelos de datos
Los mapas son modelos analógicos . Los modelos de datos espaciales son todo eso y mucho más:
Los modelos de datos no tienen escala. No se limitan a un solo nivel de escala.
Los modelos de datos se pueden explorar en muchas vistas: los usuarios pueden acercar, alejar, desplazar, ver en un vista ortogonal y en perspectiva.
Los modelos de datos son independientes de la forma en que se representan. El mismo mapa OSM se puede representar para vista diurna o nocturna, y para conductores de automóviles o ciclistas.
Los modelos de datos son expandibles. Se pueden agregar nuevos datos a medida que ingresan.
Los modelos de datos almacenan datos sin procesar. Cualquier categorización o clasificación puede ser aplicada para la visualización.
Los modelos de datos pueden almacenar explícitamente relaciones topológicas.
Los modelos de datos de información geográfica tienen un propósito diferente y extenso, que sus contrapartes análogas . Los SIG son: herramientas para almacenar, organizar, manipular, analizar y, eventualmente, también visualizar datos espaciales.
1.2.3 Modelado de datos
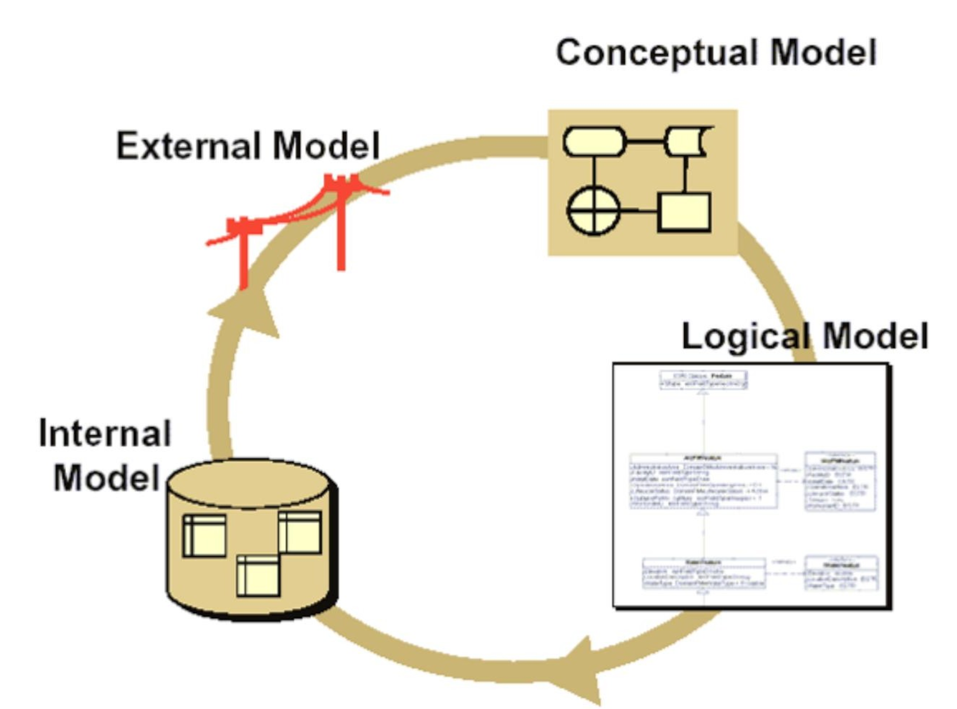
El modelado de datos es el proceso de abstracción paso a paso para representar características del mundo real en un formato digital. El proceso de modelado de datos comienza observando y dando sentido al complejo mundo real. Una vez que se implementa el modelo de datos, nos vinculamos con el mundo real para validar el modelo (Figura 1.9). Este paso es vital, ya que un modelo no es un fin en sí mismo. Siempre es un medio para razonar sobre el mundo real.
El proceso de modelado de datos consta de seis pasos:
- Modelos externos (nivel externo)
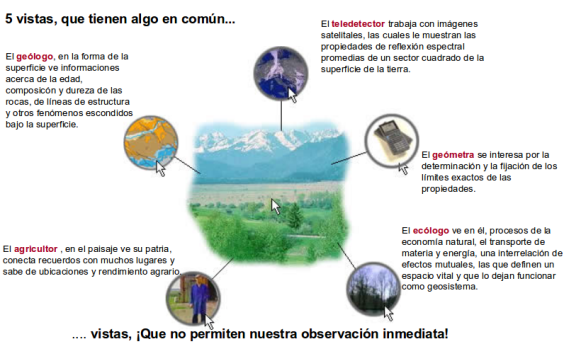
Hay tantas realidades percibidas como seres humanos en el planeta Tierra. Cada individuo tiene sus propias experiencias, recuerdos e intereses. Si le pide a un silvicultor local que describa un paisaje, obtendrá un informe completamente diferente en comparación a un geólogo, un ecologista o un agricultor, que miran exactamente la misma parte del mundo real (Figura 1.10).
- Modelo conceptual (nivel conceptual)
Los modelos conceptuales, describen los fenómenos en un sistema que son relevantes para el propósito dado. A través de esta orientación sobre el propósito, un modelo conceptual pretende sintetizar la variedad de modelos externos. El proceso comienza con la identificación de las características y relaciones geográficas relevantes en el mundo real. Un modelo conceptual se puede redactar con lápiz y papel. Sin embargo, existen notaciones gráficas que nos permiten preparar un modelo conceptual de una forma más formalizada (Figura 1.11). En las próximas lecciones de este módulo, aprenderemos a aplicar las notaciones gráficas del Lenguaje de modelado unificado (UML).
- Modelo de datos (nivel lógico)
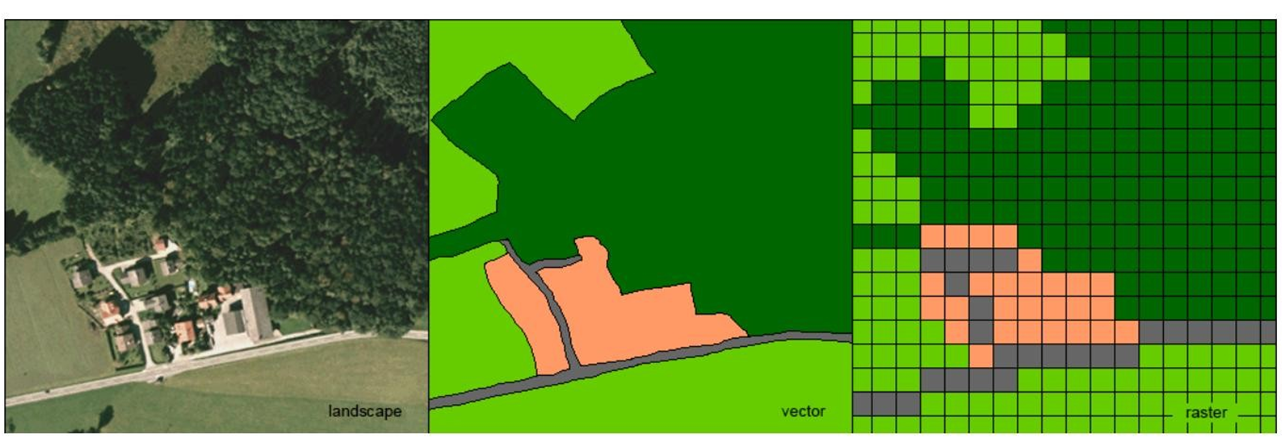
En este paso, pasamos de lo real al mundo virtual. Basados en el modelo conceptual, los modelos de datos espaciales definen las propiedades y relaciones de los objetos digitales. Al diseñar un modelo de datos, podemos hacer preguntas como “¿representaremos una ciudad como un conjunto de celdas adyacentes en un ráster que comparten el mismo atributo de uso del suelo, como una entidad poligonal o como un punto?”. La notación clásica que describe los modelos de datos son los diagramas de entidad-relación (ER). Frank (1992) distingue entre cinco modelos principales de datos espaciales. Todos ellos tienen ubicación, propiedades geométricas e información de atributos opcionales, algunos también contienen información topológica:
- Los modelos de teselación regulares: son rásteres con celdas rectangulares o cuadrículas hexagonales.
- Los conjuntos de puntos: consisten en puntos espaciados regular o irregularmente, donde el espacio en entre se interpola.
- Los modelos de espagueti: son modelos de datos vectoriales, en los que las líneas y los polígonos son simplemente construidos a partir de una lista de puntos conectados.
- Gráfica: es una red de nodos (=puntos) que están conectados con dirección o bordes no dirigidos (=líneas).
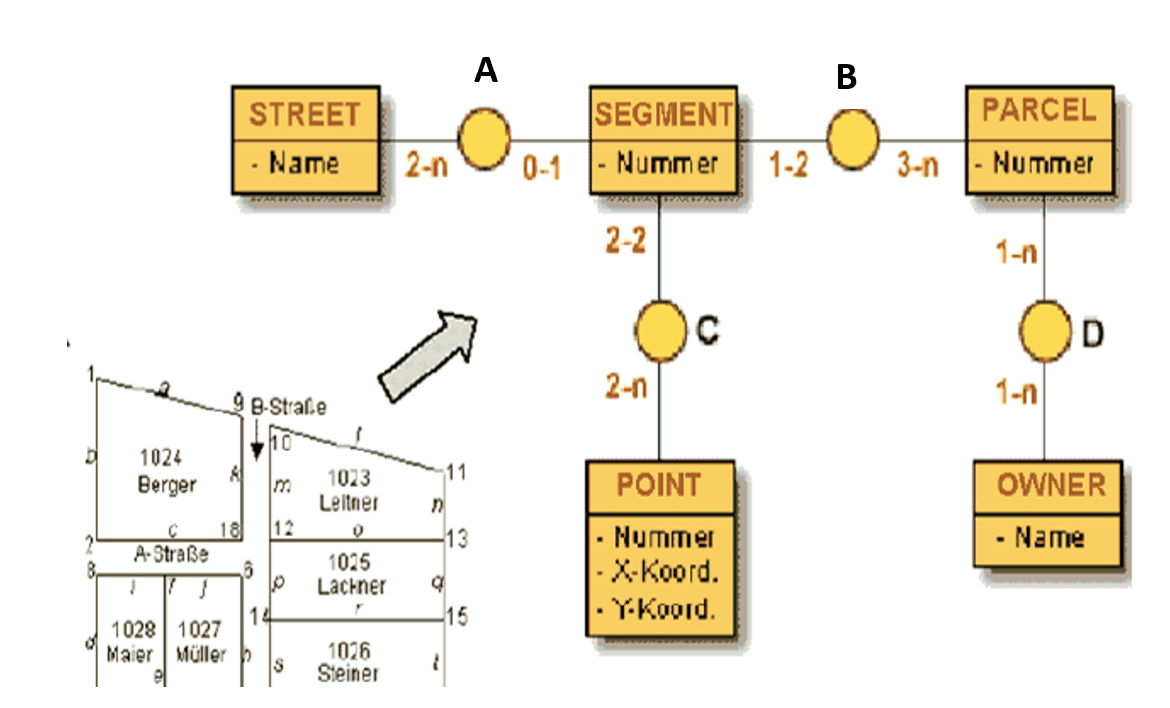
- Modelo de datos topológicos: es un modelo de datos vectoriales que no solo almacena la geometría, sino también relaciones topológicas.
- Estructura de datos (nivel interno)
En este paso, se elige una estructura de datos espaciales apropiada para codificar el modelo de datos de manera legible por computadora. Las estructuras de datos se ocupan de la optimización de la implementación en relación con el rendimiento y la utilización del almacenamiento (Frank 1992). Las estructuras de datos ejemplares que implementan modelos ráster son la codificación fila por fila, la codificación de longitud de ejecución o los esquemas de almacenamiento jerárquico, como Quadtrees. Veremos las estructuras principales para datos ráster y vectoriales en lecciones posteriores de este módulo.
- Formato de datos
El formato es la codificación Open Source o propietaria de los datos reales en un archivo o base de datos. Algunos ejemplos son formatos de archivo como .shp, .kml, .json para datos vectoriales y .asc o .tif para datos ráster. Más allá del formato de archivo, también existen estándares de intercambio que no solo entregan los datos codificados, sino también el modelo subyacente. El ejemplo más destacado en el mundo GIS, es el lenguaje de marcado geográfico (GML) el cual se verá más en detalle en lecciones posteriores.
- Validación del modelo
En este paso final, revisamos y probamos si el modelo de datos implementa correctamente el modelo conceptual (verificación) y si cumple el propósito para el que lo creamos (validación). La verificación pregunta si el modelo se implementó correctamente, mientras que la validación verifica si el modelo implementado es adecuado para el propósito. Si el modelo de datos es válido, podemos usarlo para nuestra aplicación que apoya la toma de decisiones en el mundo real.
Esta es la razón, por la que podemos pensar en el modelado de datos como una actividad cíclica en lugar de una actividad lineal (Figura 1.12).