5 Interpolación espacial
5.1 Introducción
Interpolación es un término comúnmente entendido pero su uso varía en diferentes contextos. En esta lección tratamos con la interpolación espacial enfocada en un caso bi-dimensional donde valores discretos son interpolados en puntos individuales, o donde una superficie continua es creada en base a un conjunto de puntos con datos conocidos. Simplemente, la interpolación puede ser entendida como una predicción o estimación espacial basada en puntos de muestra.
En este sentido, no estamos hablando de interpolación de series de tiempo o de isopletos (líneas de contorno) para visualizar las superficies. En realidad, vemos a la interpolación como un método para estimar el valor en un punto específico, basados en valores conocidos recolectados a través de observaciones en puntos vecinos.
La interpolación representa un campo comprensivo de métodos usados frecuentemente en el análisis espacial. En esta lección proveemos una visión general, pero al mismo tiempo detallada, que incluye los principios básicos de la interpolación espacial. Este conocimiento es una extensión de lo que usted quizá ya haya escuchado sobre métodos de interpolación en estadísticas espaciales.
El uso de métodos de interpolación es propenso a errores debido al uso no crítico de las configuraciones originales de los parámetros. Es por esto por lo que la atención principal en esta lección se enfoca en el entendimiento de la teoría que está detrás de las técnicas de interpolación comúnmente usadas.
Ejemplo de una problemática
La superficie de terreno es un ejemplo típico de una superficie continua en su mayor parte, la cual cambia sus valores de atributo en el espacio. Las superficies temáticas sin embargo son a menudo basadas en relaciones complicadas (ej. datos climatológicos o datos del tiempo, nivel del agua subterránea) donde:
- El estado y el desarrollo de la superficie cambia con el tiempo;
- El montaje de una red de observación densa y ubicua es demasiado costoso, peligroso o no viable desde el punto de vista social
Por todo esto, las mejores ubicaciones para mediciones adicionales o recolección de datos necesitan ser determinadas (ej. la ubicación para un barreno con la mínima profundidad de perforación para alcanzar el nivel del agua subterránea para construir un pozo).
5.2 Principios de Interpolación
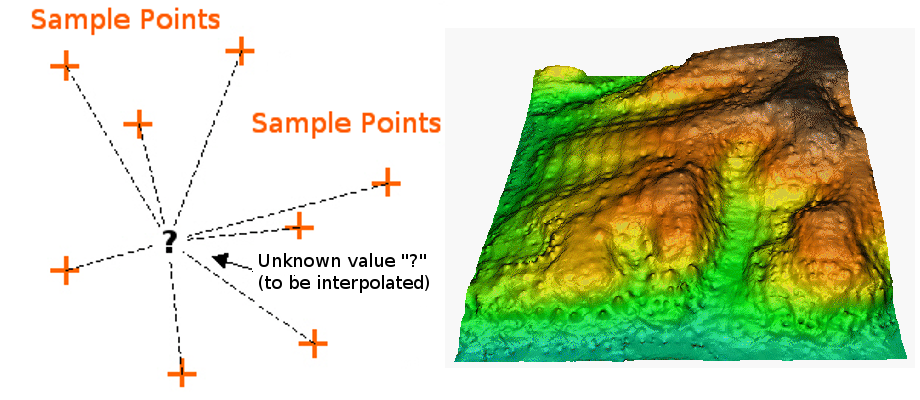
Los métodos de interpolación espacial son predicciones de valores de atributo exactos en ubicaciones sin muestreo de mediciones recolectadas en puntos dentro de una misma área.
Generalmente asumimos que hay una superficie temática o una superficie topográfica continúa con la cual debemos tratar, donde los valores de atributo varían continuamente en el espacio. Así que, teóricamente, entre dos puntos vecinos podemos siempre insertar otro punto cuyo valor de atributo es el intermedio de los dos puntos vecinos. Piense sobre la primera ley de la Geografía de Tobler que afirma que las cosas cercanas están más relacionadas que las cosas distantes. Esta suposición es la básica para las técnicas de interpolación: el valor de atributo en un punto interpolado será más similar a los puntos de medición que están más cerca de éste que los que están más distantes.
Los diferentes métodos de interpolación comienzan de diferentes suposiciones y por ende producen diferentes resultados. Es la tarea principal del analista espacial el escoger el método y la asignación de parámetros más apropiados para una tarea dada a fin de obtener el mejor valor aproximado posible.
En todo caso, los puntos de muestreo tienen que estar esparcidos sobre el área considerada para que puedan proveer la mejor cobertura. Si la predicción es hecha en base a los puntos vecinos que están alrededor, hablamos de Interpolación. Si el valor aproximado es hecho para puntos más allá o fuera del rango de los puntos vecinos, hablamos de extrapolación.
La interpolación es un procedimiento de predicción o estimación. El resultado de una interpolación no es un valor exactamente correcto (en realidad a veces es completamente incorrecto). Es decir, es un aproximado -un valor predicho- producido al aplicar un método apropiado con los parámetros escogidos correctamente (Figura 5.3). En consecuencia, para cualquier conjunto de puntos de muestreo, diferentes métodos de interpolación van a producir diferentes resultados.

En los paquetes de software de SIG disponibles comercialmente los parámetros de entrada iniciales o por definición (default) para varios métodos de interpolación generalmente tienen valores iniciales (default) aceptables. Sin embargo, a menudo es confuso para el usuario cuál es la o las suposiciones del método escogido y qué ajustes con respecto a los parámetros necesitan y pueden ser hechos.
La resolución de una superficie de interpolación se puede aumentar potencialmente sin límites. Siempre podríamos insertar otro punto entre dos puntos vecinos, cuyo valor de atributo se encuentra entre los valores de los dos puntos vecinos para proporcionar una apariencia más suave de la capa resultante.
La escala de medición para datos recolectados y datos que van a ser procesados juega un papel muy importante en muchos métodos de análisis cuantitativo. Esto también es verdad para la interpolación. Entonces asumimos que todos los datos recolectados o medidos están disponibles en una escala métrica (i.e. medible). Es crucial que el cálculo de los valores medios ponderados, que es la base de la mayoría de las técnicas de interpolación usadas, pueda ser realizado en una escala métrica.
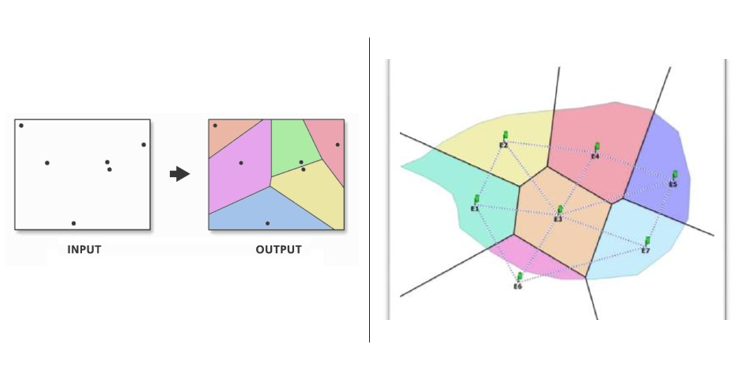
Si los valores recolectados son a nivel nominal, el cálculo de su valor medio no tiene sentido. En estos casos la técnica de los Polígonos Thiessen puede ser aplicada: para cada punto que su valor necesite ser estimado solo su punto vecino es considerado y su valor medio es adoptado. Una interpolación así está basada en el criterio del vecino más cercano (ver Figura 5.4).
Antes de profundizar en el tema de la interpolación, explore los principios de la interpolación más a fondo en el con GISnelda y GISbert.
5.2.1 Global vs Local
Uno de los criterios para distinguir los métodos de interpolación es si la interpolación estima tendencias en todo el área de estudio (interpolación global) o hace uso del principio “cuanto más cerca, más similar” (interpolación local).
El principio “mientras más cerca, más similar”, en un enfoque de interpolación, puede ser implementado a través de dos mecanismos:
- La elección de puntos de medición cerca del punto que su valor necesita ser estimado
- La ponderación de estos puntos de medición inversos a la distancia: mientras más pequeña la distancia del punto de medición, más alta su ponderación.
La interpolación en el sentido local usa este principio de la distancia inversa. La interpolación global, por otro lado, estima un espacio más grande o tendencias globales (en lugar de calcular el posible mejor estimado local). En tal tendencia espacial se espera la detección de una estructura total que indica la variación espacial de un tema particular, y la predicción de valores en puntos individuales se vuelve menos importante.
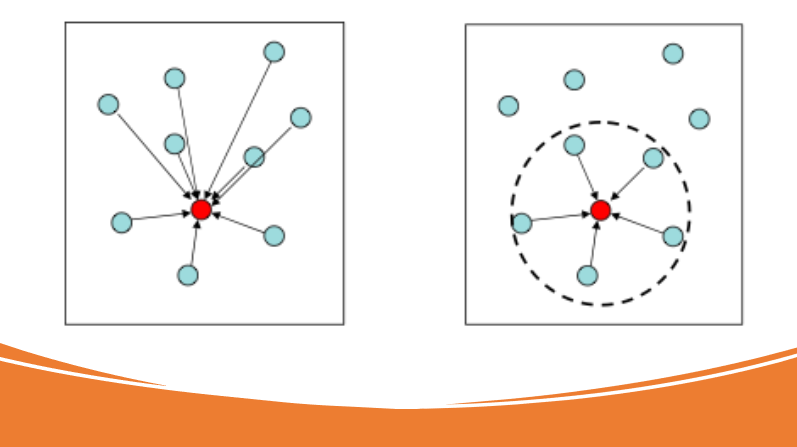
En la Figura 5.5 ponga atención a la elección de los puntos de medición que están considerados en cada proceso de interpolación y note las diferencias. Ahora pregúntese, qué valor sería más cercano al real? Es difícil de decir, ya que depende del tipo de datos o variables que se quiere interpolar.
5.2.2 Exactitud Vs. Aproximación
Uno de los criterios para distinguir los métodos de interpolación es si la superficie de interpolación reproduce los puntos de muestra exactos o solo sus estimados.
Si los valores en los puntos de muestra son relativamente exactos (precisos y certeros), repetibles y casi sin errores, un interpolador exacto debe ser aplicado. No obstante, si los valores en los puntos de muestra varían fuertemente de medición a medición tiene sentido no forzar la superficie de interpolación para que “pase” por estos puntos. Es mejor pensar en que la superficie debe estar cerca (aproximada) a los valores de medición empíricos.
La Figura 5.6 reppresenta muy bien la diferencia entre interpolación exacta y aproximada. La superficie interpolada pasa o no pasa a través de todos los puntos de los datos originales dependiendo del enfoque exacto o aproximado usado, respectivamente.

Mientras que la interpolación global es un algoritmo aproximado, los algoritmos de interpolación local a menudo son interpoladores exactos. Un ejemplo de un método de interpolación local aproximada son los splines B, que discutiremos con más detalle a continuación. IDW y Spline son interpoladores exactos típicos. Discutiremos estos métodos (y otros) con más detalle a continuación.
5.2.3 Validación
El resultado de una interpolación siempre es una estimación que tiene cierta incertidumbre inherente. Para un conjunto dado de puntos de muestra, diferentes métodos de interpolación producirán diferentes resultados. Por lo tanto, la calidad de la interpolación sólo puede ser controlada a través de mediciones adicionales tomadas en puntos fuera del conjunto utilizado en la interpolación. Los valores interpolados pueden ser comparados con estas mediciones independientes. Además de este control empírico, otras medidas pueden ser tomadas: por ejemplo, cuanto mayor sea la distancia entre el punto con el valor estimado y un punto con un valor medido, mayor será la probabilidad de una gran diferencia entre el estimado y el valor real en estos puntos. Entonces podemos determinar una superficie de distancia para los valores de puntos estimados que muestran zonas donde probablemente los valores de peor calidad de interpolación pueden ser encontrados.
5.3 Algoritmos de interpolación
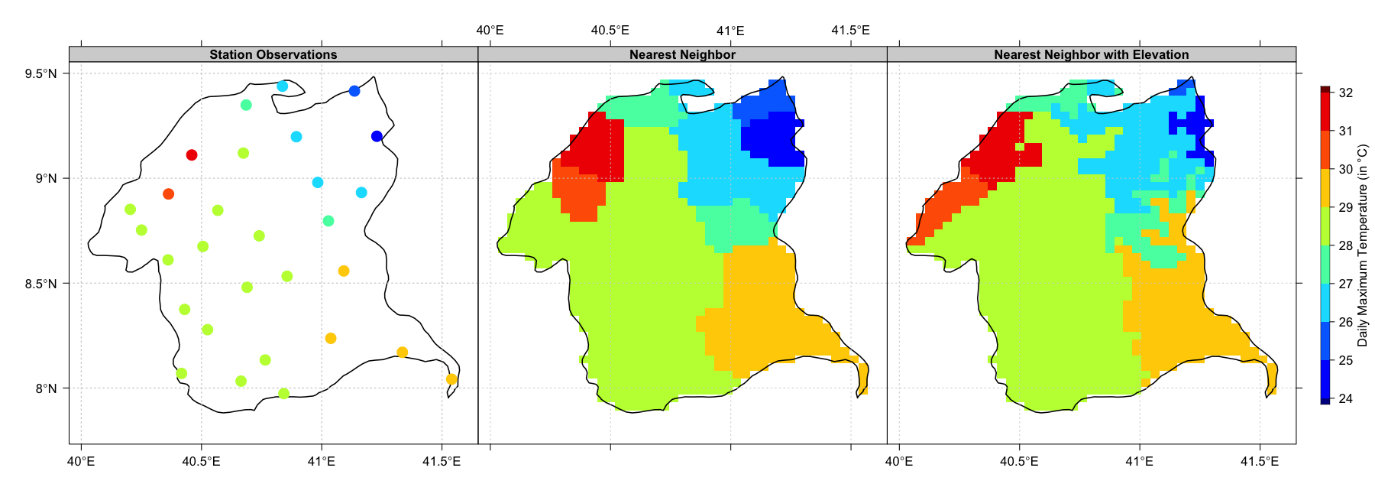
5.3.1 Interpolación por el vecino más cercano
La interpolación por el vecino más cercano es una interpolación local que asume que el valor estimado toma el valor del punto de muestra más cercano. La superficie resultante son los polígonos de Thiessen que ya hemos visto cuando discutimos el análisis basado en la distancia. Un ejemplo de interpolación por el vecino más cercano se da en la Figura 5.7, que mapea la aparición de la helada invernal en Illinois, EE.UU.
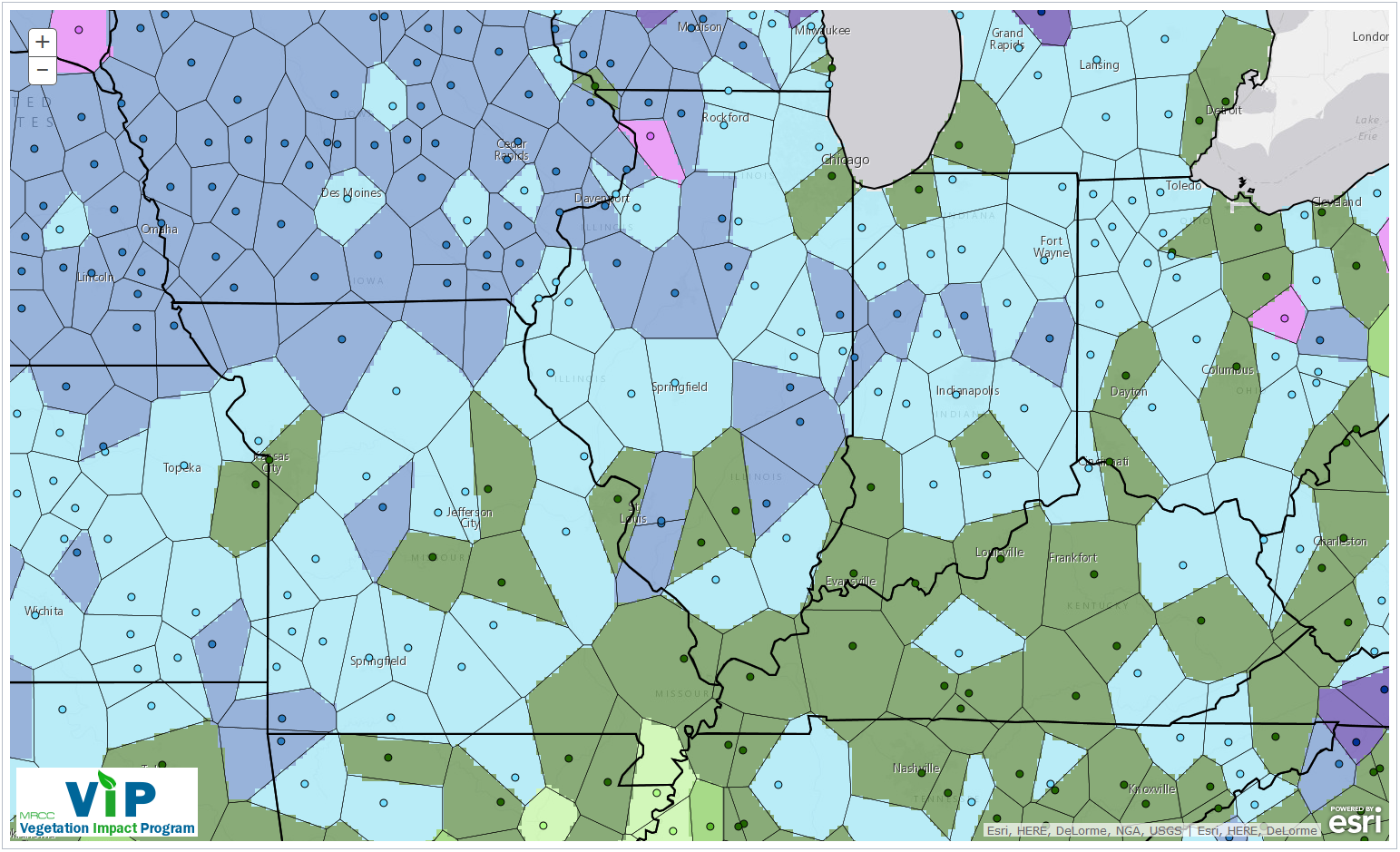
Este método simple no siempre se clasifica como un algoritmo de interpolación. Sin embargo, el principio subyacente es el mismo. Partimos de un conjunto de puntos y aplicamos un algoritmo para estimar valores en toda una superficie.
Hay dos casos en los que el vecino más cercano es la mejor (y única) opción para llegar a una superficie a partir de mediciones puntuales. Primero, en casos en los que el atributo de interés es nominal. En segundo lugar, donde el fenómeno de interés es discreto y no cambia de forma continua en la superficie. Esto es más probable que sea el caso de los datos en escala ordinal. En la Figura 5.7, los autores del estudio argumentaron que se eligió la interpolación por el vecino más cercano, porque la aparición de la helada es un fenómeno discreto que está principalmente gobernado por el sombreado topográfico local.
Las técnicas de interpolación métrica, en cambio, calculan valores medios ponderados entre los puntos de muestra. Por lo tanto, la escala de medición del atributo interpolado también es métrica. La escala de medición es, por lo tanto, lo primero que hay que comprobar antes de elegir un algoritmo de interpolación.
5.3.2 Interpolación por vecinos naturales
Los vecinos naturales son puntos que pertenecen a todos los polígonos de Thiessen que serían vecinos de un nuevo polígono de Thiessen que se construye alrededor de un punto de interpolación. El peso de la interpolación se determina entonces por la proporción de superposición entre los polígonos de Thiessen existentes y el nuevo que se crea (Figura 5.8).
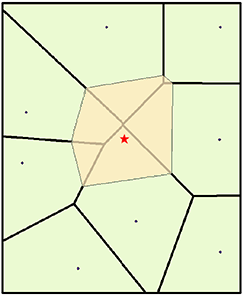
Para mas explicación visual y agradable del concepto de interpolación por vecinos naturales, consulte la Ayuda en línea de ArcGIS Pro sobre cómo funciona la interpolación por vecinos naturales.
5.3.3 Interpolación bilinear
La interpolación bilinear es el caso más sencillo de interpolación local y métrica en una superficie 2D. En la imagen siguiente queremos estimar el valor justo en el medio entre dos mediciones. Es plausible esperar un valor aproximadamente promedio para la precipitación, si no hay otra información disponible.
Observa la imagen de la Figura 5.9: ¿cuál sería el valor esperado para el círculo rojo vacío en esta imagen?
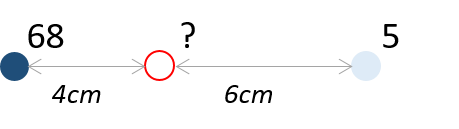
El valor resultante de una interpolación lineal entre los dos puntos vecinos es una media ponderada, donde los pesos se derivan de la distancia inversa entre la ubicación de la muestra y el punto interpolado. Aquí, es el 60% del valor 68 y el 40% del valor 5:
\[? = 0.6 * 68 + 0.4 * 5 = 42.8\]
En un plano bidimensional, tenemos que considerar dos direcciones. Mira la Figura 5.10: ¿cómo calcularías el valor del círculo rojo?
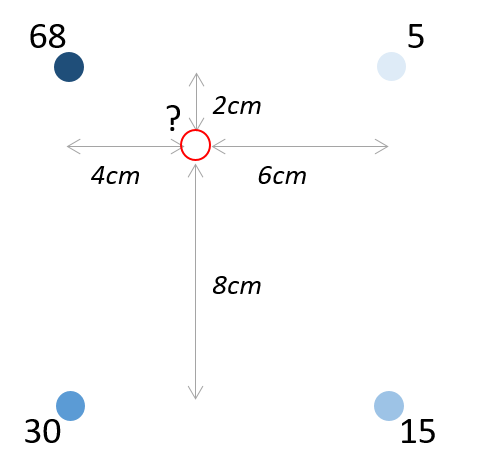
La solución de una interpolación bilinear implica dos pasos. Primero, interpolamos a lo largo del eje x. Ya sabemos que el valor interpolado entre 68 y 5 es 42.8.
\[? = 0.6 * 68 + 0.4 * 5 = 42.8\]
Podemos calcular más adelante que el valor interpolado a lo largo del eje x en la línea inferior entre los valores 30 y 15, lo que resulta en 24:
\[? = 0.6 * 30 + 0.4 * 15 = 24\]
Ahora, interpolamos a lo largo del eje y, entre 42.8 (ponderación del 80%) y 24 (ponderación del 20%). El valor interpolado es 39.04:
\[? = 0.8 * 42.8 + 0.2 * 24 = 39.04\]
5.3.4 Interpolación bicúbica
La interpolación bilinear produce transiciones bruscas en los puntos de muestra. Para evitar discontinuidades abruptas, la interpolación bicúbica ofrece una alternativa (visualmente) más agradable con transiciones continuas. En este enfoque, se ajustan ecuaciones polinomiales a los puntos. La Figura 5.11 visualiza la interpolación bicúbica en comparación con las técnicas de vecino más cercano y bilinear.
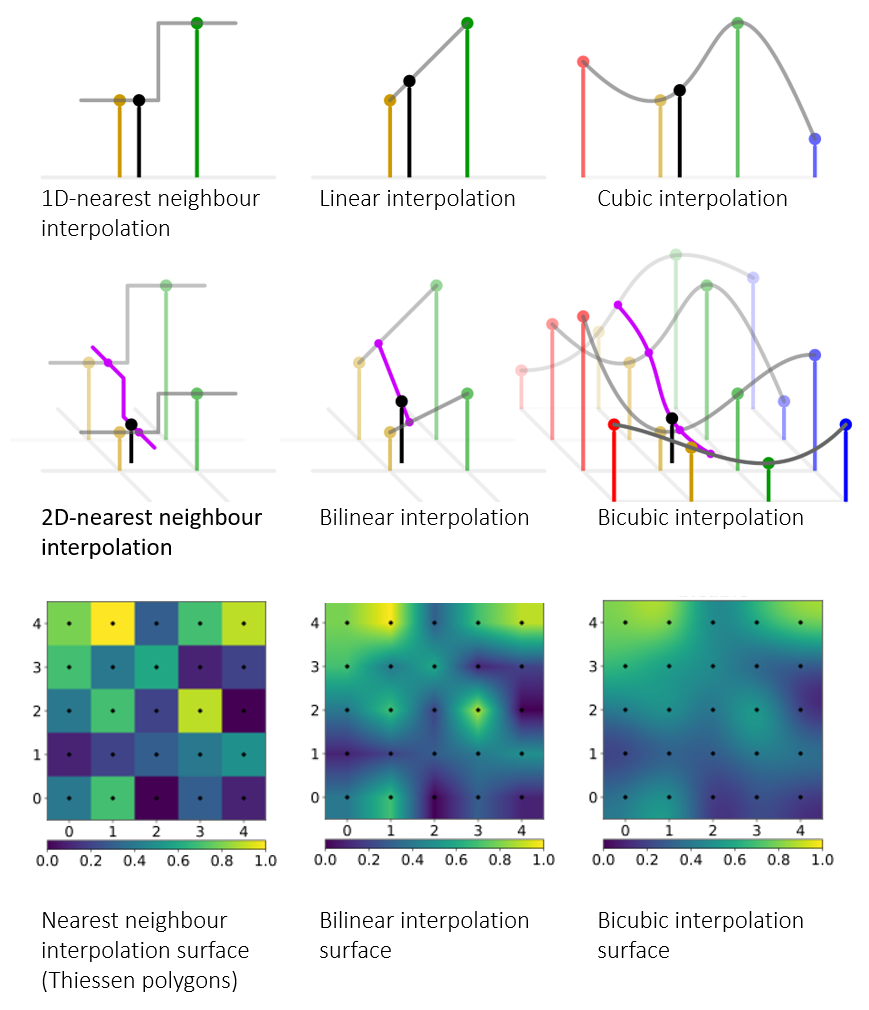
Aunque la apariencia visual parece más suave, este algoritmo tiene algunos problemas. Para ajustarse a todos los puntos vecinos, la ecuación polinomial puede producir sobresaltos, es decir, mínimos o máximos más allá de los puntos medidos. Si bien es perfectamente posible que realmente haya valores por encima y por debajo de los valores medidos, estos sobresaltos a veces producen artefactos no deseados, especialmente cuando se utilizan polinomios de orden superior. Especialmente en regiones mal muestreadas y del uso de polinomios de alto orden pueden surgir graves problemas.
5.3.5 Ponderación de distancia inversa (IDW)
Hasta ahora, hemos asumido que los puntos están distribuidos de forma regular. Este es el caso de las encuestas sistemáticas y los datos ráster y de imágenes cuadriculados. Akima (1978) desarrolló un método para aplicar la interpolación bidimensional a puntos distribuidos irregularmente. Sin embargo, este algoritmo conocido como interpolación de Akima, no está ampliamente implementado en el software SIG.
El enfoque estándar para interpolar puntos irregulares es la Ponderación de Distancia Inversa (IDW). La Ponderación de Distancia Inversa (IDW) es uno de los métodos de interpolación más flexibles y simples. Por eso es el más utilizado entre los métodos de interpolación. IDW se basa en la suposición de que “cuanto más cerca, más similar”. Cuanto más cerca esté un punto estimado de un punto de muestra, sus valores serán más similares (Figura 5.12).
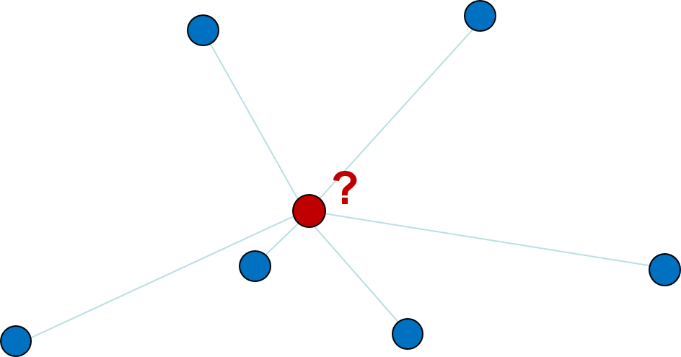
IDW es una técnica de interpolación local que considera su vecindad al estimar el valor de un punto. Este vecindario debe definirse a través de un radio, un número (mínimo) de puntos de muestra o una combinación de ambos. Un valor interpolado se calcula entonces como la media ponderada de los valores de los puntos de muestra vecinos. El peso es la distancia inversa al punto de muestra vecino.
Muchos fenómenos están gobernados por efectos de decaimiento de la distancia no lineales, como por ejemplo la intensidad del ruido o las distancias de viaje de los clientes a las tiendas de comestibles. Para tener en cuenta el fenómeno específico que un analista quiere interpolar, la distancia inversa se puede calcular a una potencia. Cuanto mayor sea el parámetro de potencia, más brusca será la caída a lo largo de la distancia. La Figura 5.13 muestra un ejemplo del efecto de decaimiento de la distancia para cuatro sectores minoristas (Klaesson y Öner 2014).
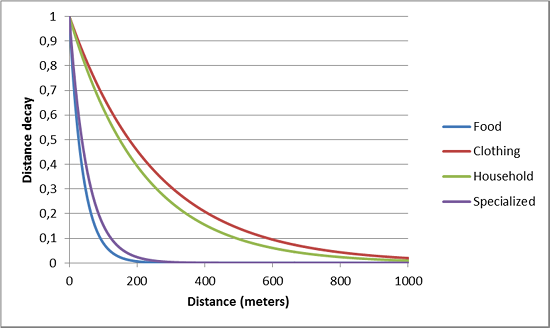
Mapeado al espacio geográfico, la disminución brusca a lo largo de la distancia da lugar a nítidos ojos de buey alrededor de valores muy altos o bajos. La Figura 5.14 muestra el efecto típico de ojo de buey de la interpolación IDW.
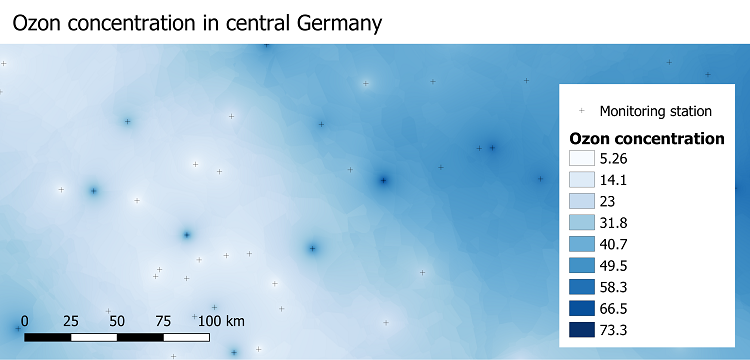
Por la importancia de la Ponderación de Distancia Inversa (IDW) vamos a resumir este método otra vez, destacando sus pasos principales. El método IDW entonces sigue el siguiente proceso:
- Encuentra los puntos de muestra vecinos de la ubicación “blanco” (ej. a través de n vecinos más cercanos o radio de búsqueda r)
- Encuentra la distancia de cada punto de muestra a la ubicación blanco.
- Pondera cada punto de muestra de acuerdo con el inverso de su distancia desde la ubicación blanco-tomada (Figura 5.15).
- Hace un promedio de los valores de atributo de los puntos de muestra y asigna el valor resultante a la ubicación blanco.
5.3.6 Spline
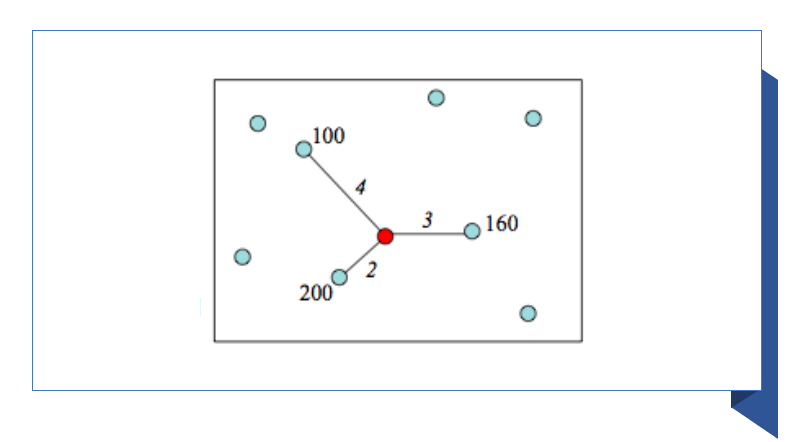
Además de la interpolación bicúbica, las splines cúbicas son un algoritmo alternativo para generar superficies de interpolación suave para la interpolación local. El término “spline” deriva de las reglas elásticas que se han utilizado para los dibujos técnicos a mano (Figura 5.16).

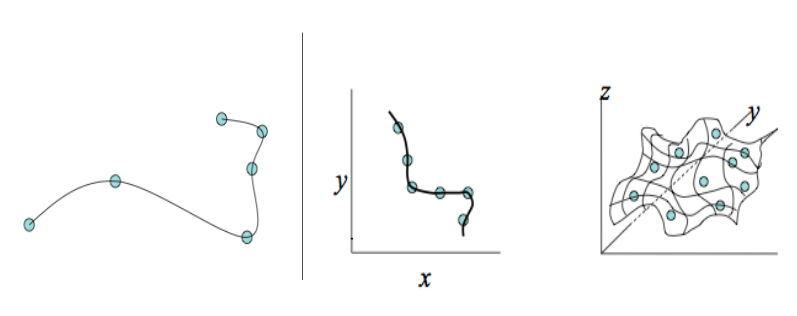
Los splines son entonces muy útiles para encajar las superficies suaves sin breaklines y discontinuidades (Figura 5.17). Este será fuertemente suavizado en aquellas ubicaciones donde la superficie tiende a ‘balancearse’ debido a la sobreestimación o subestimación de los valores. Una ‘visualización’ popular de un Spline es una banda de caucho extendida sobre los puntos de muestra. Las ponderaciones asignadas pueden ser interpretadas como tensión en estos puntos; mientras más alta la tensión, mayor es la extensión y curvatura en los puntos de valor extremo.
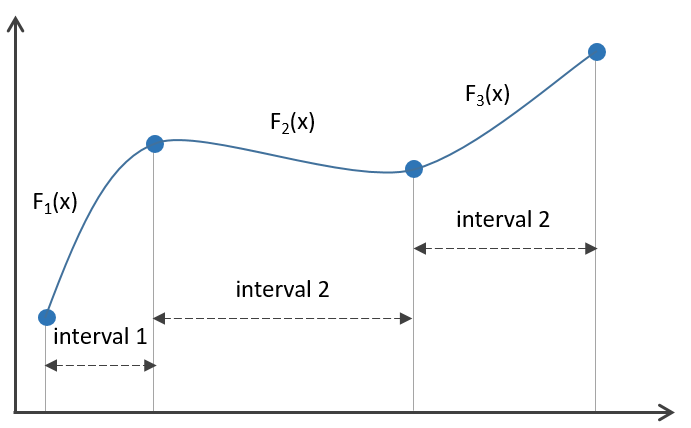
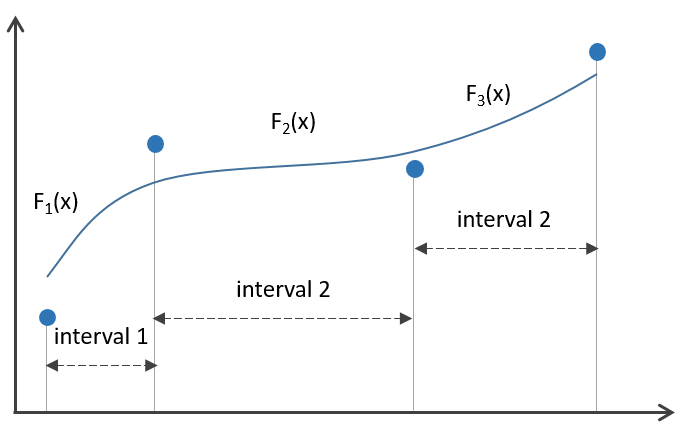
Matemáticamente, una spline es una ecuación polinomial en trozos, como se representa en la Figura 5.18, donde las splines cúbicas usan ecuaciones polinomiales de tercer orden. Esto significa que no hay una sola ecuación polinomial que tenga que pasar por todos los puntos a la vez, sino que hay varios polinomios apilados: uno para cada segmento entre los puntos de muestra. El resultado es una superficie lisa sin sobresaltos.
La interpolación de B-splines (Figura 5.19) es otro algoritmo polinomial en trozos. Sin embargo, a diferencia de las splines cúbicas, son interpoladores aproximados, que no pasan exactamente por los puntos de muestra.
Estos conceptos de interpolación de splines se han desarrollado aún más añadiendo restricciones adicionales y funciones de regresión. Los conceptos matemáticos son complejos y se implementan diferentes algoritmos en diferentes paquetes de software SIG.
Si estás interesado en los algoritmos subyacentes de los tipos de splines que se implementan en ArcGIS, echa un vistazo a Cómo funciona Spline.
Se muestra en la Figura 5.20 un ejemplo de interpolación con el método IDW. Se puede usar cualquier archivo de datos con coordenadas (x, y) y con el dato Z correspondiente a la variable que se quiere interpolar.
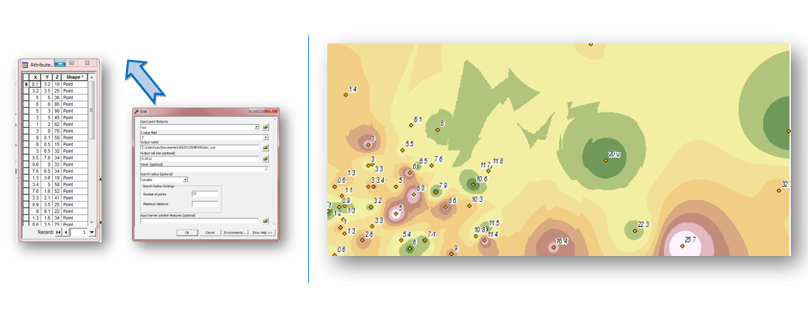
Observa que comparando con la Figura 5.21, la variación de la superficie en la zona donde hay mayor número de puntos de muestreo. Ahora observe los resultados usando los mismos datos, pero con el método Spline.
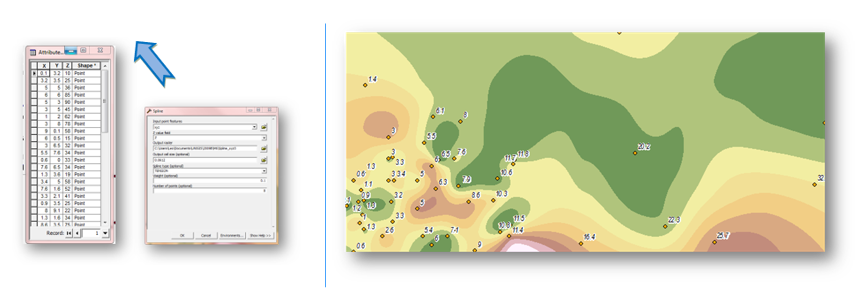
Se puede además variar los valores del vecindario para representar mejor la realidad de la variable en estudio. Al comparar ambos métodos se puede observar los distintos resultados que se puede obtener. Puede generar su propia base de datos con números al azar para poder empezar a probar con estos métodos. O mejor aún tratar de obtener datos de precipitación, de altitud u otras variables en la zona de su interés, y probar estos métodos.
5.3.7 Superficies de Tendencia (Trend Surfaces)
Las superficies de tendencia son una técnica de interpolación global. Expresan un patrón global que es válido para toda el área de estudio, y se ignoran las heterogeneidades locales. Se espera que una tendencia espacial detecte una estructura general, que indica la variación espacial de un tema particular. La predicción de valores en puntos individuales se vuelve poco importante.
Con las superficies de tendencia se pueden hacer declaraciones como estas:
- La precipitación aumenta de SW a NE.
- El nivel del agua subterránea en las inmediaciones del pozo ha disminuido drásticamente.
- A lo largo de una costa, se observa una amplitud de temperatura más baja (ancho de banda de variación).
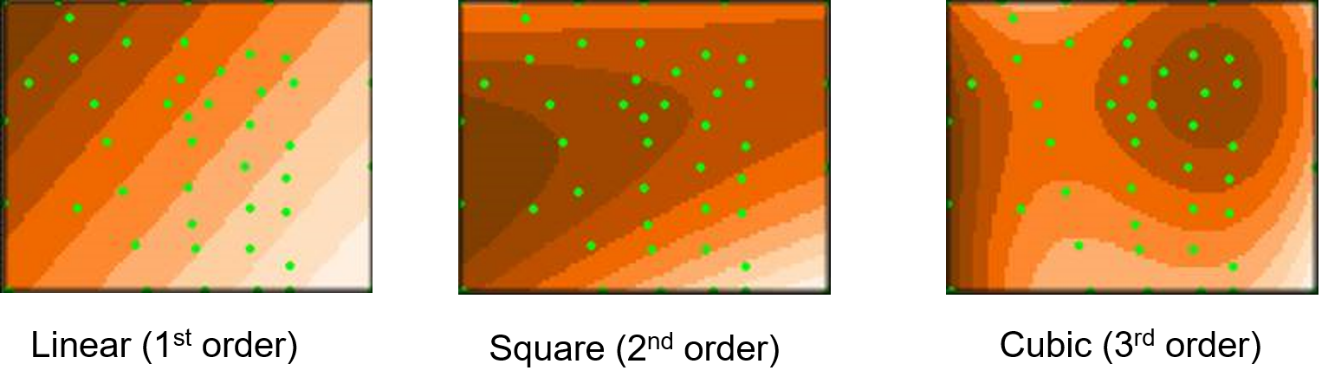
Las superficies de tendencia se calculan ajustando una ecuación polinomial para todos los puntos de muestra en una interpolación aproximada. Dependiendo del orden de la ecuación polinomial, la superficie de tendencia puede ser lineal, cuadrada o cúbica (Figura 5.22). En teoría, también son posibles polinomios de orden superior, pero se desaconseja encarecidamente su uso. Los polinomios de cuarto orden o más altos son propensos a generar picos extremos incorrectamente, especialmente cerca del límite o en áreas con poca densidad de muestreo.
5.3.8 Kriging
El Kriging, que lleva el nombre del estadístico sudafricano Danie Krige, es otra técnica de interpolación global que considera todos los puntos en el área de estudio para estimar una superficie de interpolación. Sin embargo, a diferencia de las superficies de tendencia, el Kriging tiene como objetivo una estimación lo mejor posible a nivel local. El punto fuerte del Kriging es que es un método geoestadístico que ajusta la función de decaimiento de la distancia con los datos de los puntos de muestra.
Es una técnica avanzada que requiere un buen conocimiento del trasfondo geoestadístico. Sin embargo, si se aplica adecuadamente, este enfoque supera claramente a todos los demás métodos de interpolación. Afortunadamente, los paquetes SIG cada vez más apoyan al usuario en el proceso exigente de ajuste de parámetros con la ayuda de rutinas de optimización. El Kriging asume que la variabilidad espacial del fenómeno observado es homogénea en toda la superficie, de modo que en todas las ubicaciones de la superficie se pueden encontrar los mismos valores de varianza. Esto significa que el Kriging no es muy adecuado si los patrones de proceso de segundo orden difieren en el espacio, o si los puntos de muestra están muy agrupados.
Un importante resultado del Kriging, además de una superficie interpolada, es el mapa de probabilidad. Esto indica qué tan bien se realiza una estimación en una ubicación particular al mostrar errores de estimación. Estos errores se pueden derivar del variograma y se definen como el valor de la diferencia al cuadrado del valor estimado y el valor medido.
Si quieres profundizar en temas de interpolación avanzados como el Kriging, consulta el módulo “Estadística espacial”.
5.4 Conceptos adicionales
5.4.1 Anisotropía
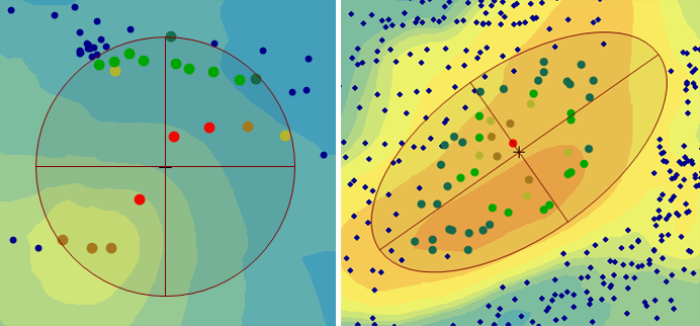
La isotropía significa que un fenómeno se propaga uniformemente en todas las direcciones, mientras que la anisotropía se refiere a un fenómeno que se propaga de forma dependiente de la dirección. Las dunas de arena de la Figura 5.23 fueron moldeadas por vientos de una dirección constante, lo que ha formado este hermoso ejemplo de anisotropía.

Si los datos que queremos interpolar son anisotrópicos, es importante tener en cuenta la distribución de los puntos. En tales casos, tenemos que estirar el eje de búsqueda a lo largo de la dirección del fenómeno y dividir aún más el vecindario de búsqueda en sectores direccionales para obtener buenos resultados (Figura 5.24). El vecindario debe ser lo suficientemente grande como para garantizar que haya un número mínimo de puntos de muestra disponibles para parametrizar cada cuadrante individual.
5.4.2 Líneas de ruptura
Hay casos en los que una superficie se extiende de forma continua sobre un área más grande, pero pueden producirse discontinuidades en lugares concretos. Tales discontinuidades pueden ocurrir, por ejemplo, a través de bordes abruptos en el paisaje (crestas), divisorias geológicas, muros o vallas artificiales (Figura 5.25).
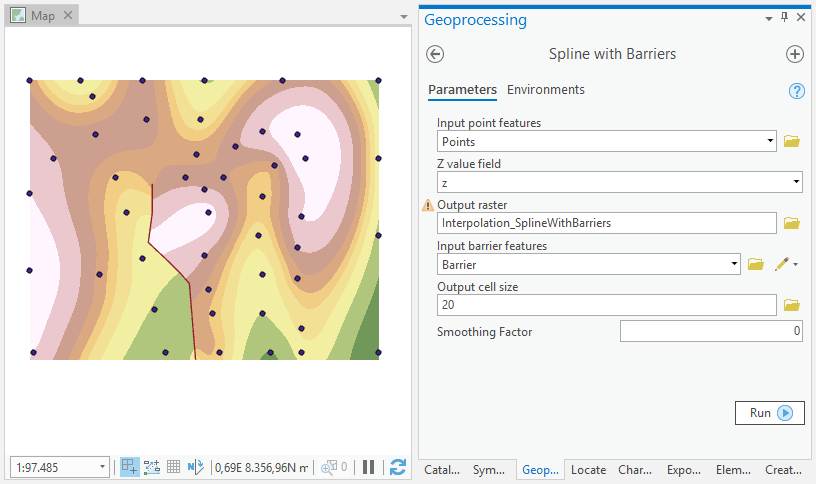
Estas discontinuidades, por supuesto, también deben conservarse después de la interpolación. Para lograr esto, solo los puntos de muestra del lado respectivo de la línea de ruptura deben utilizarse en el proceso de interpolación. No se utilizan puntos que estén más allá de esta línea para estimar un valor.
5.4.3 Lineas de Contorno (Contour Lines)
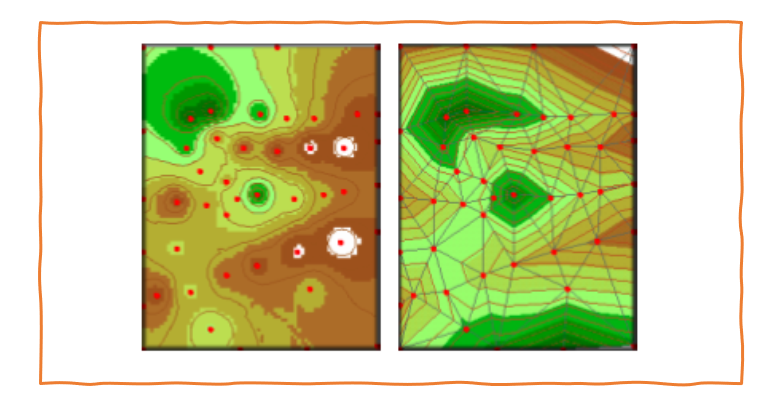
Por el hecho de estar cerca de completar la cobertura del tema de interpolación, mencionamos brevemente de las líneas de contorno (isopletos). Estrictamente hablando, las líneas de contorno son un método de visualización, pero es a menudo e incorrectamente referido como interpolación.
Una comparación de una de una capa ráster y un isopleto TIN ‘interpolado’ del mismo conjunto de datos (ver Figura 5.26) ilustra cuán diferentes pueden ser los resultados. Es entonces altamente recomendado NO interpolar superficies de líneas de elevación digitalizadas (mejor dicho: prohibido;), sino usar los puntos originalmente medidos para generar la interpolación.