7 Definiendo la estadística espacial
7.1 Introducción a estadística
7.1.1 Campos de la estadística
La estadística trata todos los asuntos de relacionados con los datos, donde se incluyen la colección, la organización, la sintetización, la interpretación y la toma de decisiones basadas en esos datos. Los cálculos numéricos y los gráficos que salen a partir de todos esos procesos orientan la toma de decisiones (Figura 7.1).
Como se muestra en la Figura 7.1, la estadística se divide a su vez en dos grandes campos Estadística descriptiva y Estadística inferencial
La Estadística descriptiva se utiliza para resumir y describir los datos de forma cómoda, utilizable y comunicable. Si estamos analizando los resultados electorales, por ejemplo, una estadística descriptiva podría ser el porcentaje de votos que apoyan al Partido A, o el porcentaje medio de no votantes por unidad electoral. Para obtener una imagen completa de los datos se utilizan varias estadísticas descriptivas.
La estadística inferenciale se utiliza para generalizar una interpretación más allá del conjunto de datos examinado. Para ello, el conjunto de datos examinado es un pequeño subconjunto, denominado muestra, de un conjunto de datos mayor, denominado población. Los resultados de una encuesta electoral que se realiza antes de las elecciones son una muestra de la población y pueden utilizarse para hacer inferencias sobre los resultados finales.
7.1.2 Tipos de variables
Las variables son propiedades o características de un objeto medido que pueden tomar distintos valores (a diferencia de las constantes como \(π\) que no varían). Las variables se distinguen por las siguientes propiedades:
- Independientes o Dependientes (también llamadas: Explicativas o de Respuesta)
- Cualitativa o Cuantitativa.
- Discreta o continua
Las variables independientes son las que se manipulan, mientras que las variables dependientes sólo se miden o registran. Por ejemplo, examinamos la edad de un organismo (variable independiente/explicativa), para hallar, estimar o medir su altura (variable dependiente/de respuesta).
Una variable cualitativa es principalmente no numérica. Ejemplos de datos cualitativos son el color del pelo, los nombres de las ciudades y el tipo de coche que se conduce. Cuando se presentan datos cualitativos, suelen resumirse mediante totales o porcentajes. Por ejemplo, el 35% de las personas del estudio tienen el pelo rubio. A menudo se asigna un número a los datos cualitativos y se introducen en una base de datos con fines informativos. Pero si se recogieran datos sobre el color del pelo, ¿tiene sentido calcular un color medio? No.
Así que hay que tener cuidado con el uso y la presentación de los datos cualitativos. Aunque se asigne un número a los datos cualitativos, no tiene sentido calcular un color medio. En su lugar, es probable que informes del número o porcentaje de personas que son negras, morenas, rubias, etc. Tu edad o tu peso, tu tensión arterial y la temperatura de tu despacho son variables cuantitativas.
Además, las variables cuantitativas pueden ser discretas o continuas. Una variable discreta tiene un valor específico o finito. Se puede contar. Ejemplos de variables discretas son el número de mesas de su oficina, la cantidad de memoria (en bytes) de su ordenador, el número de páginas de un guión o el número de personas matriculadas en un curso de estadística. Una variable continua es diferente, ya que puede asumir cualquier valor dentro de un determinado rango de precisión. Dependiendo de la precisión del dispositivo de medición, su altura podría ser 1,8 m, 1,82 m, 1,824 m, etc. Las variables continuas suelen aparecer cuando se mide algo.
7.1.3 Niveles de medida
En función de sus características y de cómo se miden, los datos (y las variables) se clasifican en cuatro niveles de medición o escalas de medición diferentes (Figura 7.2).
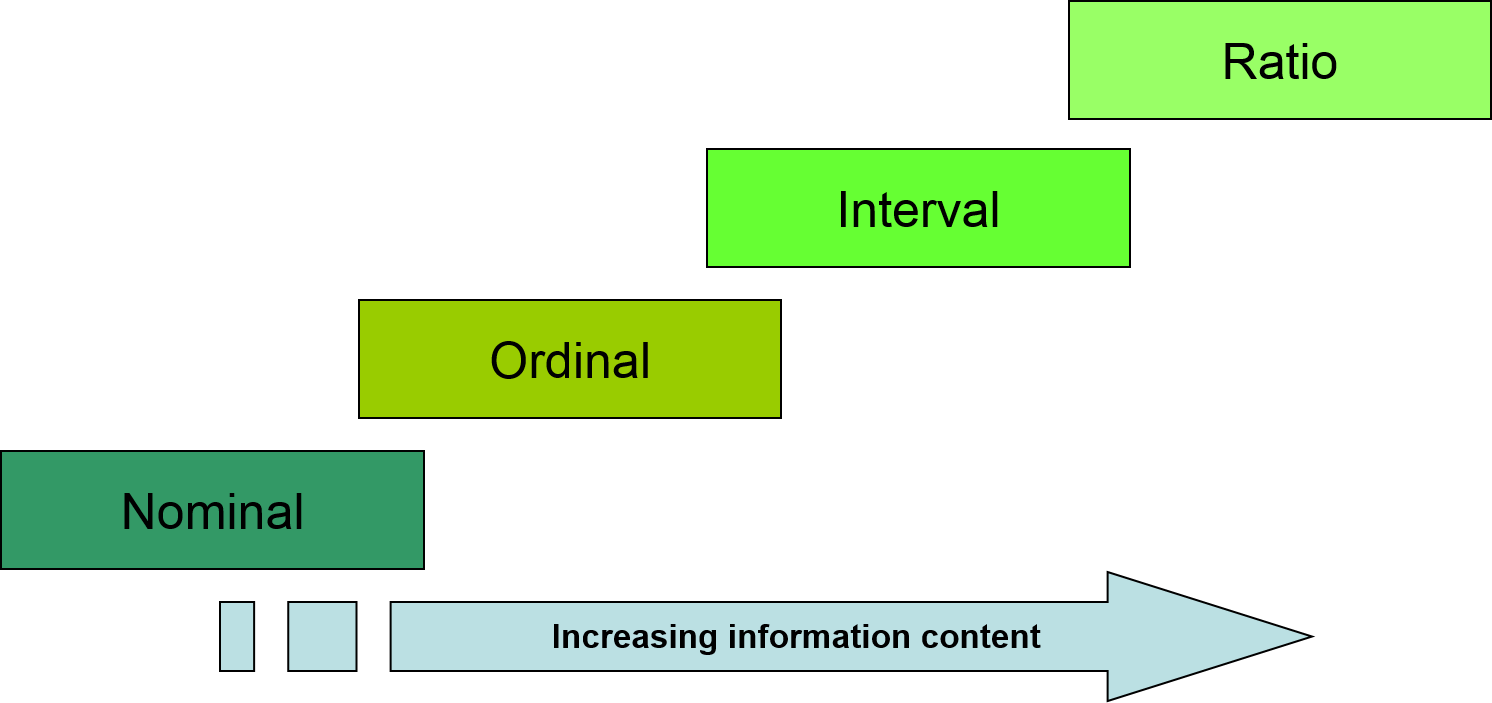
Datos de escala Nominal. Los datos nominales no tienen ningún orden. Los datos sólo pueden contarse y clasificarse por categorías o etiquetas. Algunos ejemplos de datos nominales son el sexo, el color del pelo o un tipo de uso del suelo (por ejemplo, urbanizable, industrial, etc.). Las respuestas a encuestas del tipo SÍ / NO son otro ejemplo de datos nominales. Aunque se utilicen números para clasificar los datos, los números en sí no tienen otro significado que el de etiqueta o categoría.
Datos de escala Ordinal. Los datos ordinales tienen algún tipo de clasificación u orden. Los datos ordinales tienen las propiedades de los datos nominales, pero el orden o rango es significativo. Muchos de nosotros estamos familiarizados con los datos ordinales que se encuentran a menudo en las encuestas. Por ejemplo, si en una encuesta le preguntaran su opinión sobre este curso, podría haber cinco respuestas posibles: excelente, muy bueno, bueno, regular o malo. Las respuestas tienen un rango o valor asociado. A veces se utilizan números para representar las posibles respuestas: por ejemplo, 1 = excelente, 2 = muy bueno, etc. También se trata de datos ordinales.
Datos de escala Interval. Los datos de intervalo tienen las propiedades de los datos ordinales y existe una diferencia fija y mensurable entre las variables. Los datos contienen un orden que se basa en la cantidad de una determinada característica que poseen. Con los datos de escala de intervalo, el valor cero (0) no tiene un valor significativo.
Ejemplos de datos de intervalo son la temperatura con un termómetro o las puntuaciones estandarizadas de un test. Por ejemplo, La diferencia entre 30 grados y 40 grados representa la misma diferencia de temperatura que la diferencia entre 10 grados y 20 grados.
Datos de escala Ratio. Los datos de relación tienen el nivel de medición más alto posible. Contiene, además de todas las características de los datos de intervalo, el valor cero (0) que indica que no existe ningún valor para una variable. Los datos de relación incluyen la medición de la distancia, la altura, el peso y el coste de un bien o servicio.
Por ejemplo, si hoy ha comprado un ordenador nuevo por 800 euros, y el precio de la pantalla TFT que también ha comprado es de 200 euros; como se trata de datos de razón, podría indicar que el precio del ordenador fue 4 veces el precio de la pantalla TFT 800 euros/200 euros). La diferencia más significativa entre los datos de relación y los datos de intervalo es que puedes hacer comparaciones como el precio del ordenador y el de la pantalla TFT con datos de relación, pero no puedes hacer lo mismo con datos de intervalo. ¿40°C es el doble de calor que 20°C grados? El valor numérico es el doble, pero es difícil determinar si 40°C hace el doble de calor que 20°C (de hecho, ¡no es así!).
Observe que, mediante la clasificación (binning), las escalas de medición de nivel superior pueden convertirse en escalas inferiores (pero no al revés). Como los datos de relación son, con mucho, los más comunes en geociencias, el resto de este módulo se centrará en los datos de relación.
En este apartado también se mencionan los datos cíclicos y los datos circulares. Los datos cíclicos se refieren a procesos (que pueden incluir el tiempo) y se discutirán en la lección sobre autocorrelación. Los datos circulares (también conocidos como datos direccionales 2D), que son importantes en geografía, serán considerados en el sobre análisis exploratorio de datos espaciales.
7.1.4 Usos y abusos de la estadística
La estadística es parte integrante de la vida cotidiana; por eso es tan importante conocer las fortalezas y peligros de la estadística.
Hay tres tipos de mentiras: las mentiras, las malditas mentiras y las estadísticas” - Benjamin Disraeli (Primer Ministro británico).
7.1.4.1 La interpretación si importa!
“Cuantas más escuelas hay en una ciudad, más delincuencia hay. Por lo tanto, las escuelas conducen a la delincuencia”
El ejemplo de la Figura 7.3 muestra que una interpretación errónea puede inducir a error y distorsionar la verdad. El hecho es que tanto el aumento de las escuelas como el de los índices de delincuencia se explican por el aumento de la población. En las ciudades más grandes hay más escuelas y más delincuencia. Sin embargo, la interpretación anterior insinúa causalidad aunque existe una tercera variable, la población, que puede causar ambas situaciones. Ten en cuenta que la Estadística no es sólo hechos y cifras; se trata más bien de analizar, interpretar, mostrar y tomar decisiones basadas en datos..
Fuerza - La Estadística da credibilidad a un argumento. La estadística proporciona las técnicas necesarias para reaccionar de forma inteligente y lógica ante la información.
Para evaluar las afirmaciones estadísticas siempre debes tener en cuenta
- los estadísticos presentados - media, mediana, moda y rango medio: ¿se llaman todos promedios pero dan cifras diferentes?
- las fuentes de los resultados estadísticos: ¿es la muestra lo suficientemente grande o cuál es la calidad de los datos de entrada?
- los procedimientos utilizados para generar las afirmaciones - ¿se utilizan mal los gráficos?
7.2 Estadística espacial
Ahora que ya sabe algo de estadística, puede que se pregunte: ¿y la estadística espacial? De momento, considere la estadística espacial como una estadística “normal”, pero ampliada al aspecto espacial: ¡de eso tratan la geografía y muchas otras disciplinas relacionadas con la geografía!
Las personas, los objetos físicos (¡y sus propiedades!) se encuentran en la superficie terrestre o cerca de ella y nos gustaría medir su contexto espacial e inferir procesos.
No sólo interesa la edad media de las personas en Latinoamérica. También sería bueno saber algo sobre la distribución espacial de la edad media; por ejemplo, ¿hay regiones con una población más joven? Si las hay, ¿están dispersas aleatoriamente por Latinoamérica? ¿O existe una agrupación de tales regiones o una tendencia espacial, por ejemplo, un aumento de la edad media con la latitud?
Como complemento de la estadística estándar, la estadística espacial nos proporciona métodos para cuantificar el conjunto de propiedades y relaciones espaciales.
Otro ejemplo de estadística espacial procede de la prospección de deslizamiento de tierras.
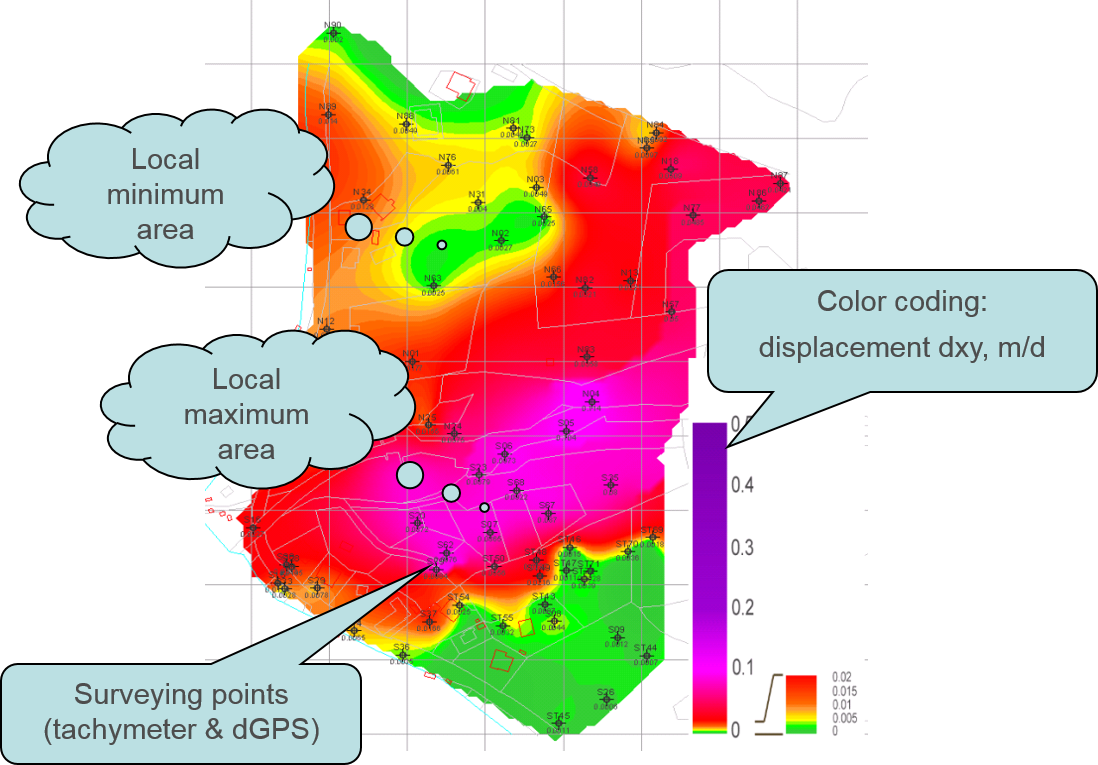
La Figura 7.4 muestra los movimientos diarios observados en un deslizamiento, con las magnitudes de desplazamiento codificadas por colores del verde (bajo) al violeta (alto). El código de colores sugiere una distribución muy variable de las velocidades de movimiento del deslizamiento, con mínimos y máximos locales pronunciados. Obviamente, resumir los desplazamientos con, digamos, 0.025 metros por día para toda la zona, no tendría demasiado sentido. Eso sólo tendría sentido si los desplazamientos fueran relativamente constantes en toda la zona. A la hora de planificar contramedidas o inferir el proceso de movimiento, necesitamos conocer la distribución espacial de los desplazamientos.
7.2.1 Estadística global/local
La estadística espacial consiste en un conjunto de técnicas y medidas globales y locales.
La medida o estadística global es un valor único que se aplica a todo el conjunto de datos. Describe el mismo patrón o proceso en toda el área geográfica y es un promedio para toda el área. El resultado de una estadística espacial global no permite sacar conclusiones sobre las diferencias regionales en el área de estudio.
Por otro lado, la medida o estadística local es un valor calculado para cada unidad de observación. Muestra que pueden darse diferentes patrones o procesos en distintas partes de la región y tiene números únicos para cada lugar/unidad. Las estadísticas locales se desarrollaron como extensiones de las estadísticas globales ya conocidas y existentes.
7.2.2 Diferencias entre estadísticas locales y globales
Características de las estadísticas globales: Resumen de los datos de toda la región, estadísticas de valor único, no cartografiables y no aptas para SIG, a-espaciales o espacialmente limitadas, hacen hincapié en las similitudes en el espacio, buscan regularidades o “leyes”.
Características de las estadísticas locales: Desagregación local de las estadísticas globales, estadística multivalor, cartografiable y apta para SIG, espacial, énfasis en las diferencias a través del espacio, búsqueda de excepciones o puntos calientes locales.
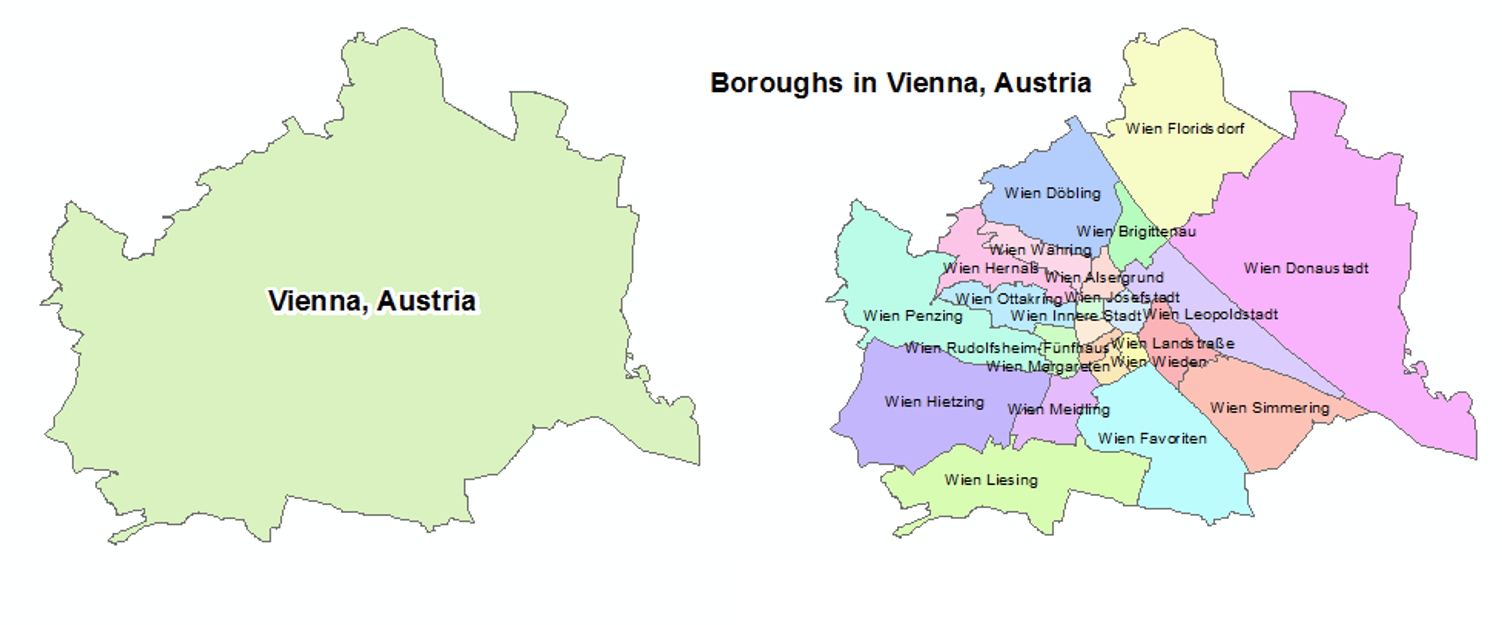
Por ejemplo, no es lo mismo mostrar el índice medio de delincuencia/densidad de población/precio de la vivienda para toda la ciudad de Viena que para cada distrito (Figura 7.5).
7.2.3 Estadística espacio-temporal
Esta animación (Figura 7.6) de un proceso de deslizamiento de tierras le ofrece un ejemplo de la evaluación estadística espacial de las velocidades de movimiento de los deslizamientos -Gesamptverschiebung (Meter / Woche) = desplazamiento total (metros / semana)- y la influencia de las precipitaciones (Niederschlag) en las mismas.
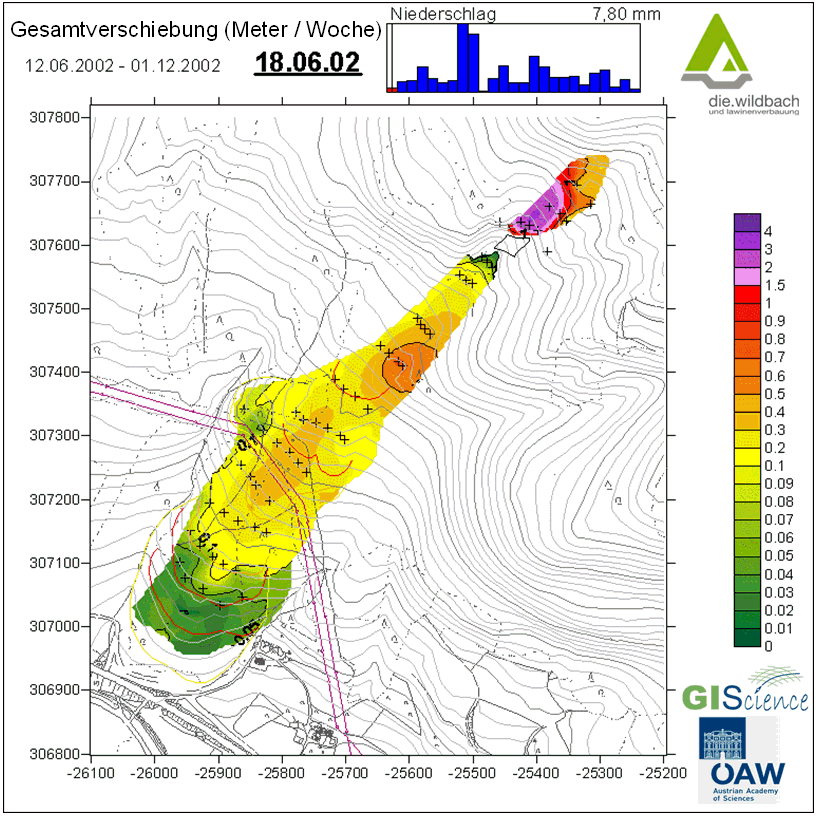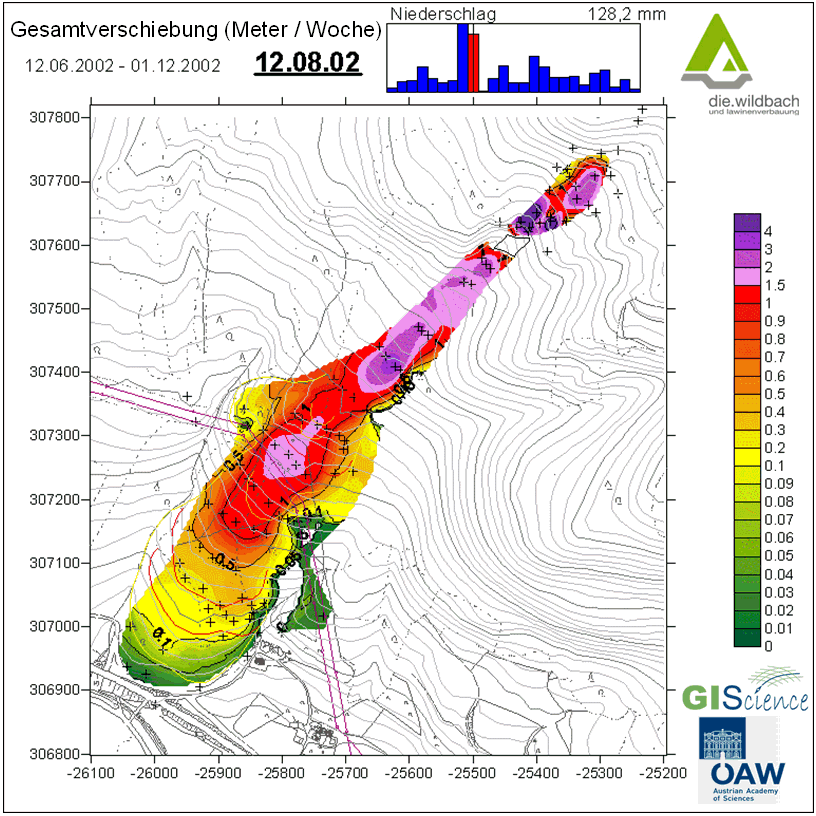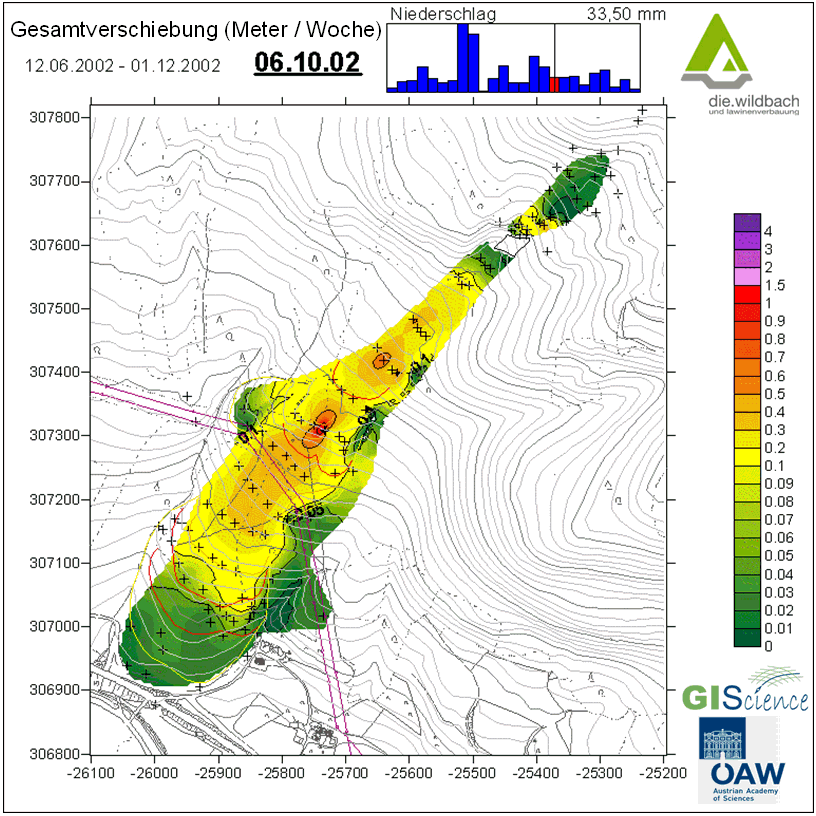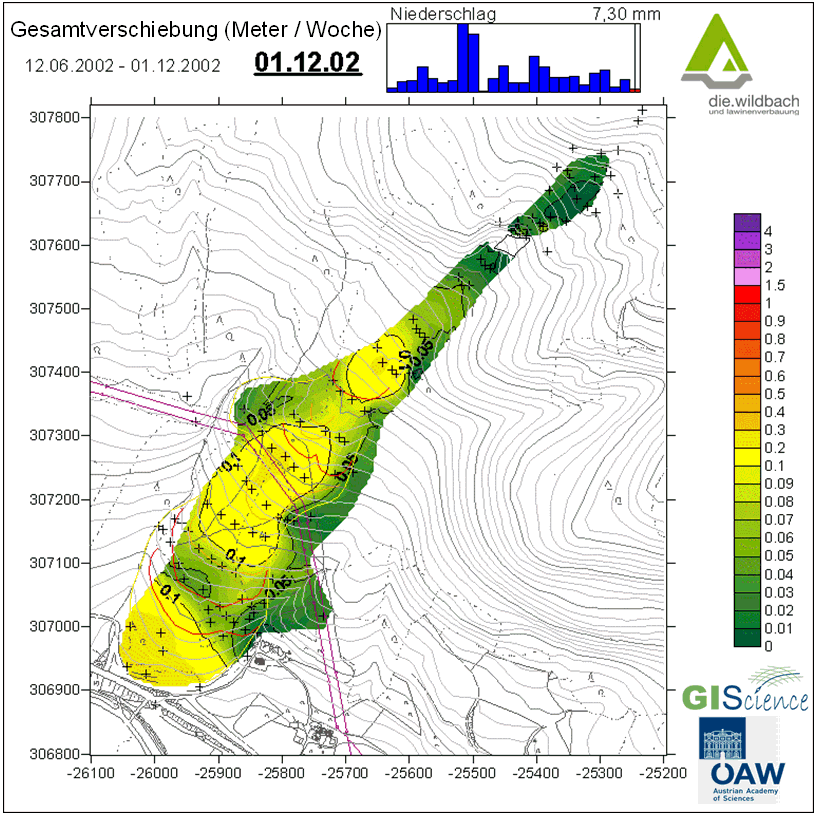
Estos dos recursos pueden servir para complementar su estudio sobre estadística y estadística espacial
- Online Statistics Education: A Multimedia Course of Study de Rice University, University of Houston Clear Lake and Tufts University. http://onlinestatbook.com/
- Quieres saber más sobre una deficiniaicón de estadística espacial, mira el trabajo de Brunsdon, Fotheringham, y Charlton (1998) en https://www.jstor.org/stable/2988625?seq=1
