4 Proyección cartográfica
El sistema de transformación de una superficie esférica a una superficie plana se denomina proyección. Dicha definición hace referencia a cualquier objeto por lo que afectará también a fotografías, imágenes de satélite, imágenes de radar o mapas en el ordenador (teniendo en cuenta que la imagen que aparece en una pantalla de un monitor es plana).
El concepto de proyección de un mapa puede imaginarse como una proyección de luz (Figura 1). Si pusiéramos una bombilla emitiendo luz en un globo translúcido y proyectáramos la imagen en una pared, obtendríamos una proyección del mapa. Y así, en lugar de proyectar una luz, los cartógrafos utilizan las fórmulas matemáticas para crear las proyecciones.
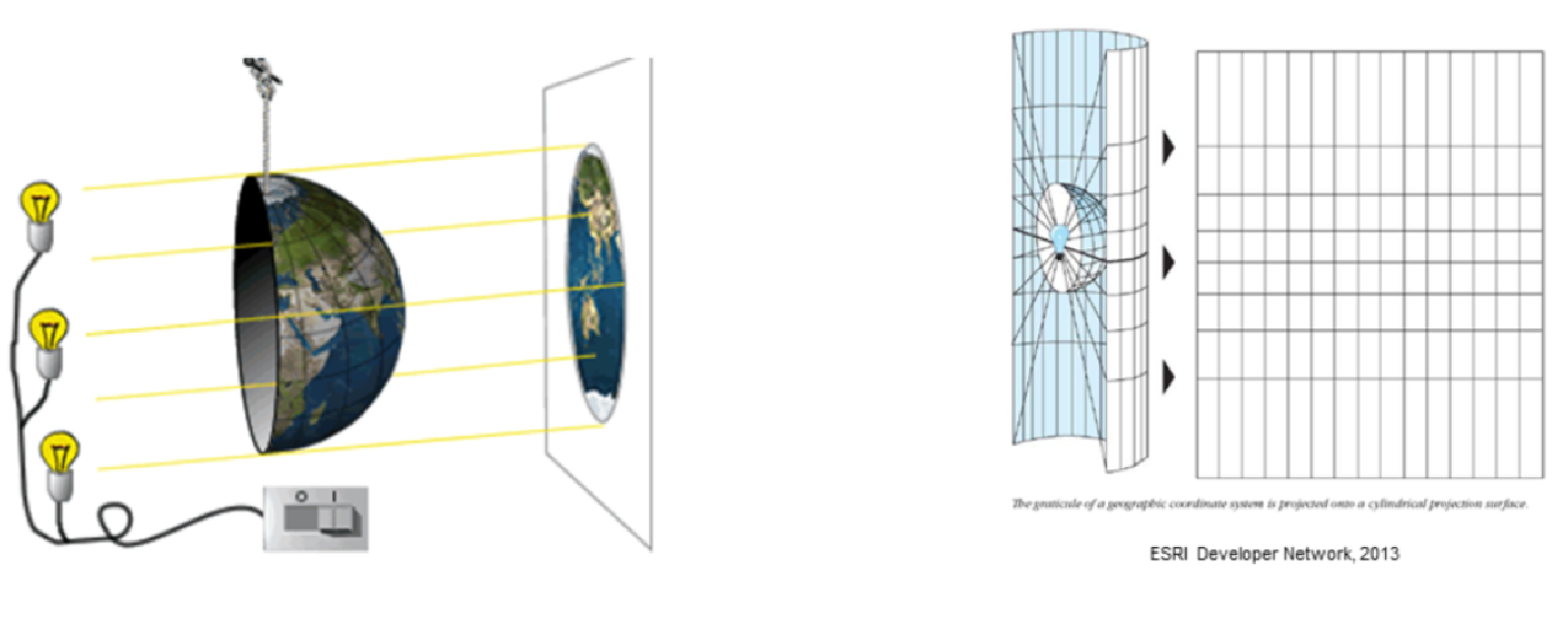
La transformación que supone la proyección de una superficie esférica a una plana sin duda provoca de algún modo una modificación en la geometría y por lo tanto alguna distorsión respecto a la realidad (Figura 4.2).

Podría parecer suficiente limitar nuestro trabajo con datos espaciales a un sistema de coordenadas geográficas. Después de todo, la ubicación de cada punto en la superficie de la Tierra se puede describir claramente de esta manera. Sin embargo, un examen más detallado revela que definir cada punto de la Tierra no es realmente posible. Esto nos lleva al tema de las proyecciones cartográficas. El problema de cómo mapear la superficie curva tridimensional de la Tierra ocurre en todas las formas comunes de visualizar datos espaciales, tanto al presentarlos en una pantalla como al producir mapas en papel. La única excepción es la representación a escala local de la Tierra en un globo terráqueo.
Comúnmente se entiende que se pierde una cierta cantidad de información original cuando se usan proyecciones, lo que resulta en inexactitud. Se utilizan diferentes enfoques (en las proyecciones) dependiendo del propósito de la presentación y de la ubicación y el tamaño del área que se representa. Por lo tanto, el conocimiento de las proyecciones comunes y su idoneidad para diferentes situaciones es uno de los principales y necesarios requisitos previos para trabajar con SIG. No es necesario memorizar cada una de dichas proyecciones, pero si tener presente que cada una de estas tiene tanto ventajas como limitaciones.
4.1 Tipos de proyecciones
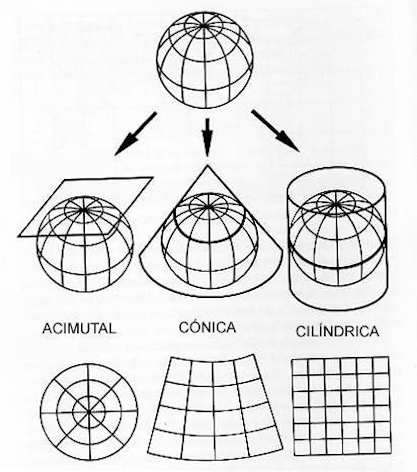
Una forma de clasificar las proyecciones de los mapas es teniendo en cuenta cómo están relacionadas la posición de un punto en la superficie del mapa y la posición en la curva terrestre (Figura 4.3). Según esto la proyección será:
- Cilíndrica: Al proyectar la superficie esférica en un cilindro
- Azimutal o Plana: Al proyectar la superficie en un plano
- Cónica: Al proyectar la superficie esférica en un cono
4.1.1 Proyección Cilíndrica
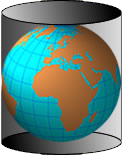
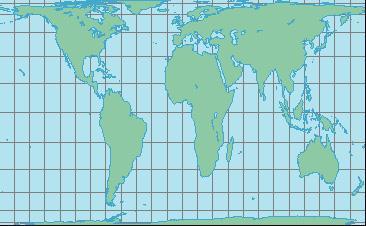
Estas proyecciones son el resultado de envolver un cilindro alrededor de la Tierra, como se muestra en la Figura 4.4, que luego se desenrolla en un plano. En su posición normal, en la que coinciden el eje del cilindro y el eje de rotación de la Tierra, el cilindro toca la Tierra en el ecuador. En este caso, la imagen resultante de las latitudes y longitudes proyectadas son líneas paralelas que se cruzan entre sí en ángulos rectos. Las proyecciones cilíndricas se utilizan para representar toda la Tierra, así como para la representación a escala continental de áreas más pequeñas. Las proyecciones cilíndricas tienden a ser conformes, pero no equivalentes.
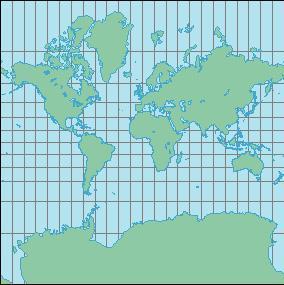
Cuando se utiliza este tipo de proyección (Figura 4.5), normalmente no se representa la Antártida
La proyección de Peter (Figura 4.6), es una proyección cilíndrica de área equivalente, utilizada en proyectos de vertiente social.
4.1.2 Proyecciones azimutales o planas

Las proyecciones azimutales también se denominan proyecciones planas (Figura 4.7). En una proyección azimutal, la gratícula de la Tierra se transfiere a un plano que normalmente se encuentra en el polo norte o sur (en lugar de acostarse a lo largo de un plano tangencial). El contacto resultante de la gratícula con el polo muestra círculos concéntricos de latitud y formas radiales - meridianos - que emanan del centro. Los ángulos entre los meridianos (azimut) en la proyección son idénticos a los de origen en la Tierra.
Las proyecciones azimutales rara vez se utilizan para representar toda la Tierra. En cambio, son adecuados para la representación de partes o hemisferios individuales.
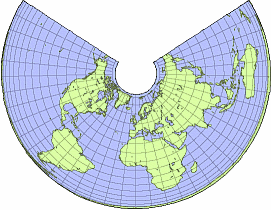
4.1.3 Proyección Cónica
En la Figura 4.8, la superficie utilizada para construir una proyección es un cono que toca un globo terráqueo a lo largo de cualquier círculo pequeño o el cono que atraviesa el globo respectivo. El cono se corta a lo largo de una de las líneas desde su vértice hasta el borde, lo que resulta en un plano de proyección con los meridianos convergiendo en el ápice y paralelos curvos. Todas las líneas se cruzan en ángulo recto (como en las proyecciones azimutal y cilíndrica).

Las proyecciones cónicas se utilizan principalmente para áreas de escala media a local. Son especialmente adecuados para regiones de latitudes medias con una gran extensión este-oeste (por ejemplo, mapa general de Austria 1: 500,000, mapa de contorno de los Estados Unidos). Tienden a no ser conformes ni equivalentes, pero suelen guardar un buen equilibrio entre estos dos extremos. La proyección de Albers (Figura 4.9) es una de las proyecciones equivalentes más utilizadas.
Volviendo a la ilustración de la Figura 4.1, hasta ahora, asumimos que la fuente de luz utilizada para la proyección estaba en el centro de la Tierra. Cambiar la posición de esta fuente de luz puede dar lugar a diferentes perspectivas en la proyección, es decir, diferentes mapeos de la gratícula sobre la superficie de proyección. La fuente de luz se puede posicionar en tres ubicaciones: el centro de la Tierra, lados opuestos de la Tierra y la ubicación infinita en el espacio (Figura 4.10).
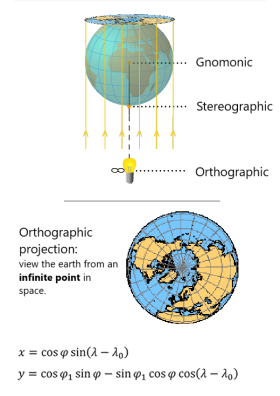
Las proyecciones cónicas y cilíndricas generalmente usan una fuente de luz que emana del centro de la Tierra. En las proyecciones azimutales (planar) se pueden ver claramente los efectos del uso de fuentes de luz en diferentes posiciones, especialmente en las proyecciones polares. Se puede ver que, en la proyección gnomónica, la mayoría de las latitudes / paralelos no son visibles en absoluto, pero los grandes círculos se representan como líneas rectas. La proyección ortográfica, por otro lado, casi se asemeja a la visión que un geógrafo esperaría al ver la Tierra desde el espacio.
La analogía con el posicionamiento de una fuente de luz se aplica bien al ejemplo de la Figura 4.5 (proyección en perspectiva verdadera); sin embargo, para muchas otras proyecciones esto no se aplica. En esos casos es necesario permitir la existencia de rayos de proyección curvos y contabilizarlos en los algoritmos matemáticos subyacentes.
4.1.4 Pseudo y otras proyecciones
Como se muestra en la Figura 4.11, estas proyecciones difícilmente se pueden describir utilizando la analogía de “iluminación de bombilla” porque no se refieren a ninguna superficie de proyección geométrica regular. Por ejemplo, una pseudo proyección puede parecer una cilíndrica con sus líneas en sus extremos curvadas hacia adentro.
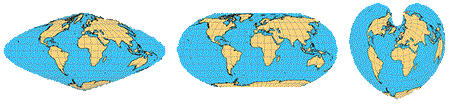
Las pseudo proyecciones se utilizan principalmente para mapear toda la superficie de la Tierra (planisferio). Dado que la mayoría de las aplicaciones SIG operan en áreas de mayor escala, las pseudo proyecciones desempeñan un papel menos importante en el contexto de los SIG.
4.2 Aspecto de la proyección del mapa
El aspecto de proyección del mapa se refiere al punto o línea (s) de tangencia en la superficie de proyección (Figura 4.12). En teoría, puede tocar o intersectarse en cualquier lugar de la superficie de proyección. La calidad de una proyección es mejor cuando la superficie de proyección toca la superficie de la Tierra. Por ejemplo, una proyección azimutal en la que el plano de proyección toca la Tierra en o cerca del polo norte da como resultado proyecciones significativamente mejores para las áreas cercanas al polo que las regiones ecuatoriales. En contraste, una proyección cilíndrica tangencial al ecuador es mejor para las áreas ecuatoriales que para una región polar.
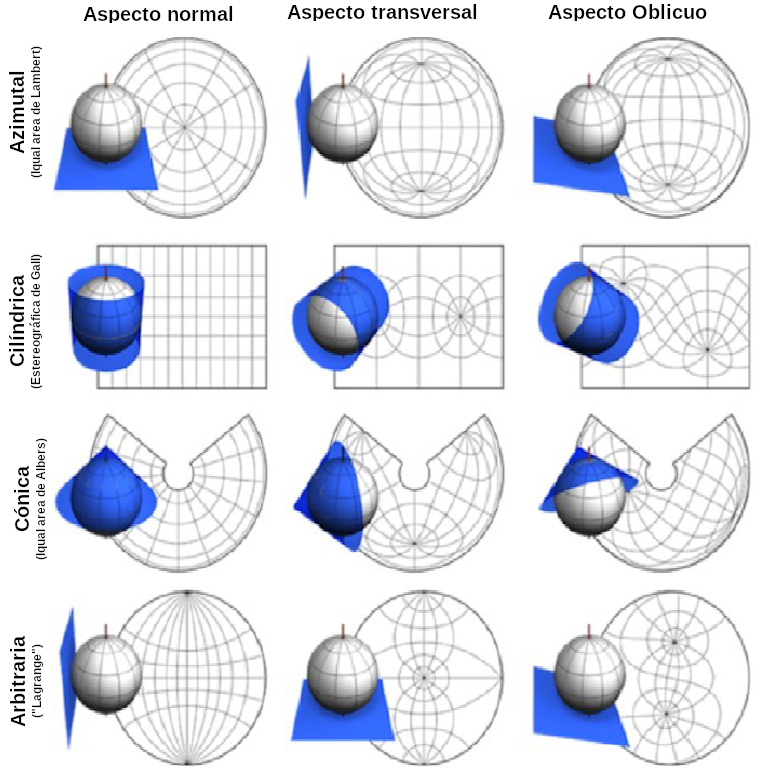
¿Cómo es que los mapas a gran escala altamente precisos se basan en una proyección cilíndrica? Por ejemplo, en Europa estamos bastante lejos del ecuador. Para proyectar cualquier parte (pequeña) de la superficie de la Tierra en alta calidad, cambiamos la posición del cuerpo de proyección (geométrico) en relación con la Tierra. Por ejemplo, con un cilindro horizontal, incluso las áreas fuera de la zona ecuatorial se representan con suficiente precisión. De esta manera es posible distinguir tres aspectos de la proyección:
- Aspecto normal: El eje del cuerpo de proyección corresponde al eje de la Tierra.
- Aspecto transversal: El eje del cuerpo de proyección es perpendicular al eje de la Tierra.
- Aspecto oblicuo: El eje del cuerpo de proyección está inclinado hacia el eje de la Tierra.
Como se muestra en la Figura 4.13, la elección de un mapa con diferente aspecto de proyección da como resultado presentaciones muy diferentes de la gratícula y la distribución de las masas de tierra. Sin embargo, las propiedades de distorsión de cualquier superficie de proyección dada permanecen sin cambios cuando se cambia el aspecto.
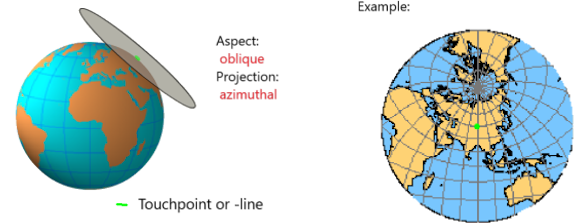
Conozca los aspectos de las proyecciones del globo en este sitio.
4.2.1 Proyecciones tangentes y secantes
Como ya sabes, hay tres tipos de superficies de proyección: un cono, un cilindro o un plano. Imagina la Tierra envuelta en una de estas superficies de proyección (desarrollables). Otro aspecto de calidad de una verdadera proyección depende de que esta superficie desarrollable solo toque la superficie de la Tierra - caso tangente - o se cruce con ella - caso secante (Figura 4.14).
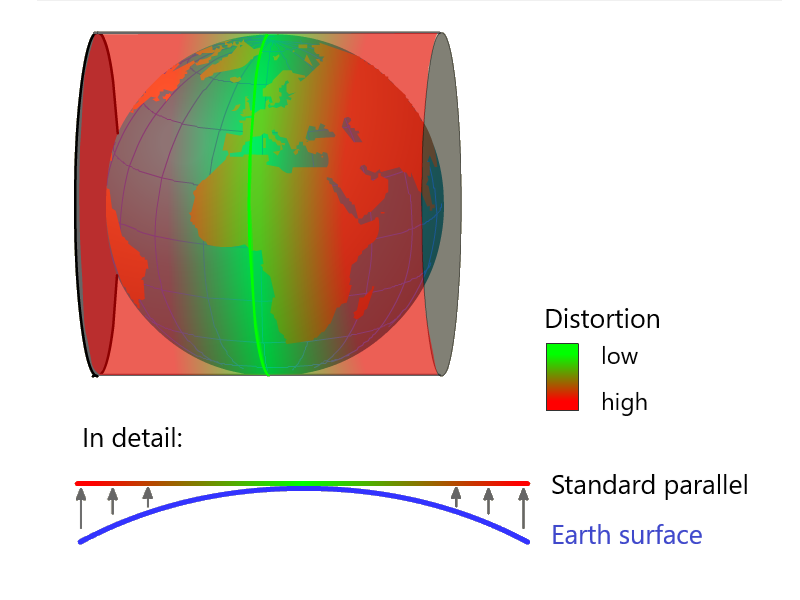
El paralelo estándar resultante es la línea de latitud donde la superficie de proyección toca el globo. Como se muestra en la Figura 4.15, una proyección cónica o cilíndrica tangente tiene un paralelo estándar, mientras que una proyección cónica o cilíndrica secante tiene dos. El paralelo estándar no tiene distorsión. La distorsión, sin embargo, aumenta hacia el medio y los bordes.
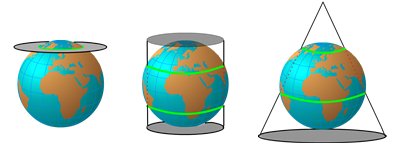
En comparación con el enfoque tangente, el enfoque secante permite casi duplicar el área a proyectar y, al mismo tiempo, preservar la calidad de la proyección. He aquí un ejemplo: antes del año 2000, para el mapa base de Austria en 1:500.000 se utilizó una proyección cilíndrica transversal (Gauss-Krüger) que cubre una zona de 3° por meridiano central. Desde el año 2000 se utiliza una proyección cilíndrica transversal (Universal Transverse Mercator – UTM) que cubre una zona de 6° por meridiano central conservando las mismas características de calidad.
4.2.2 Parámetros de proyección
Las proyecciones se utilizan para mapear el mundo entero, así como para mapear un área específica, como un continente, una zona de guerra, etc. En cualquiera de estos casos, se espera tener una proyección que sea la correcta (exacta); es decir, es preciso seleccionar una proyección para la cual se conozcan las distorsiones y que estas se mantengan al mínimo. Esto se puede lograr mediante la selección de los parámetros apropiados. Los parámetros de proyección son una serie de valores que definen una proyección en particular, que dicen cómo se relaciona la proyección con la Tierra. Los parámetros de proyección pueden indicar el punto de tangencia, o las líneas donde una superficie secante se cruza con la Tierra. También definen el esferoide utilizado para crear la proyección, y cualquier otra información necesaria para identificar la proyección.
Los parámetros de proyección son de dos tipos: angulares y lineales (Kimerling et al. 2016).
4.2.2.1 Parámetros angulares
Meridiano Central/Longitud de Origen.- es una longitud geográfica que se refiere al origen de la proyección. Tal meridiano se encuentra en el centro de la hoja de mapa resultante. El origen de la proyección es también el origen de las coordenadas x e y en la proyección. En la Figura 4.16 se utiliza como origen el meridiano 0°.
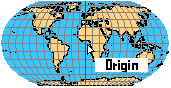
Latitud de origen / Latitud de referencia es una latitud que define el origen de la proyección del mapa. La intersección de la latitud y la latitud de origen es el origen de las proyecciones cartográficas (x, y). Un cambio de latitud de origen no afecta al contenido asignado; sólo el origen de los valores de coordenadas y cambia en consecuencia. Una excepción aquí son las proyecciones azimutales: el cambio de latitud de origen cambia la ubicación de la superficie de proyección y, por lo tanto, influye significativamente en el contenido del mapa resultante (cuerpo del mapa). Como se muestra en la Figura 4.17, el valor del parámetro de 45° indica la latitud del origen = 45°.
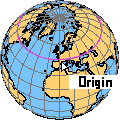
Paralelo estándar / Latitud de escala verdadera es la línea de latitud en una proyección cónica o cilíndrica en aspecto normal donde la superficie de proyección toca el globo. Una proyección cónica tangente o cilíndrica tiene un paralelo estándar, mientras que una proyección cónica o cilíndrica secante tiene dos. En el paralelo estándar, la proyección no muestra distorsión. En la Figura 4.18 se visualiza una proyección cónica con dos paralelos estándar.

Latitud del Centro/Paralelo Central – Similar al meridiano central (excepto para latitudes, por supuesto), esta latitud es la latitud media de una proyección. Su intersección con el meridiano central es el origen del punto de proyección del mapa. Se utiliza principalmente con proyecciones que tienen puntos de distorsión cero (como proyecciones gnomónicas y ortográficas). Nota: mientras que la latitud de origen no tiene que estar en el centro, el paralelo central sí.
4.2.3 Parámetros lineales
4.2.3.1 Falso este / falso norte (falso x, falso y)
Las coordenadas proyectadas (es decir, coordenadas x, y) tienen valores positivos para algunas ubicaciones y negativos para las otras. Esto depende de dónde se cruzan los ejes x e y. En los mapas publicados que utilizan coordenadas x, y como referencia, es una práctica común tener todos los valores de coordenadas positivos. Por ejemplo, si su área de interés está ubicada favorablemente, no se requiere ninguna acción al final. Puede influir en él mediante la elección del meridiano central y la latitud de origen. Una forma conveniente es el uso de valores de falso este y de falso norte: estos son dos números grandes – constantes – que se agregan a cada coordenada x e y, respectivamente. Las constantes seleccionadas son lo suficientemente grandes como para asegurarse de que todos los valores de coordenadas en su área de interés tengan un valor positivo.
Ejemplo: El sistema de coordenadas de Austria para ÖK 1:50000 tiene su origen en la intersección de cada uno de los meridianos centrales con el ecuador; por lo tanto, el valor y corresponde a una distancia del ecuador. Los valores y en Austria oscilan entre aproximadamente 5130000 y 5430000 metros. Para acelerar la escritura, se introduce el valor de norte falso de -5000000; por lo que de cada y se resta el valor 5000000 m resultando en valores con considerablemente menos dígitos.
4.2.3.2 Factor de reducción de escala
Una escala de mapa es una relación entre una distancia en un mapa y la distancia respectiva en la realidad. Debido al estiramiento y la contracción que se produce al transformar la superficie elipsoidal de la Tierra en un plano, la escala del mapa variará en el área mapeada (es decir, en todo el mapa). Por lo tanto, distinguimos entre 2 tipos de escalas (Kimerling et al. 2016):
La escala real (verdadera) es la que podemos medir en cualquier punto del mapa. Varía de un lugar a otro y es una consecuencia directa de la distorsión geométrica del aplanamiento de la Tierra.
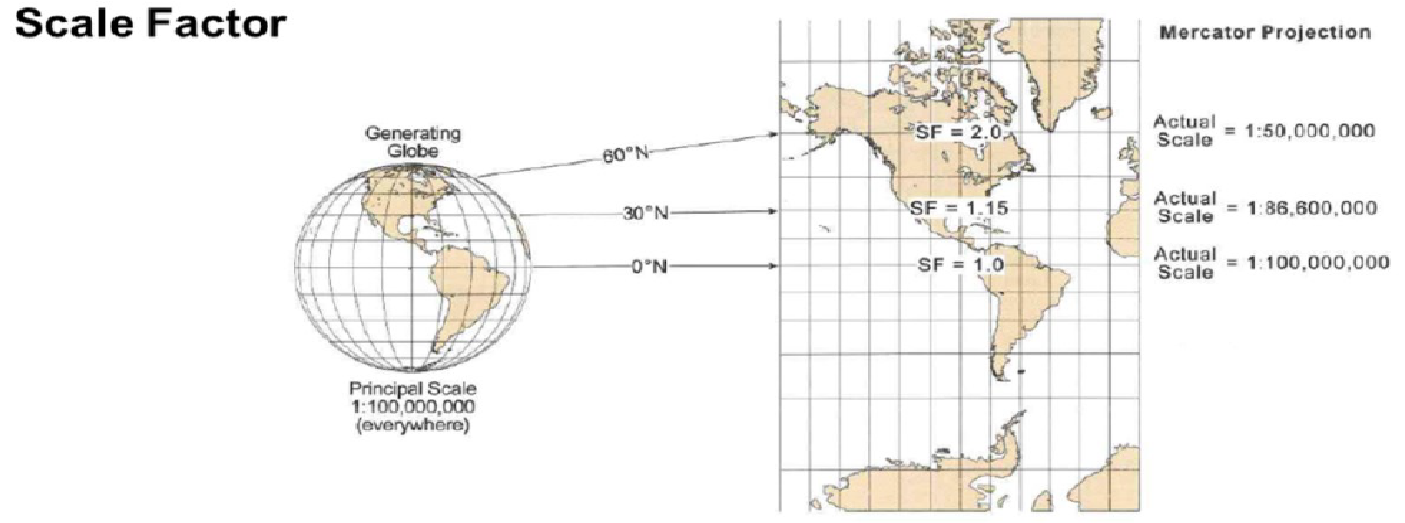
La escala principal es la escala deseada de un mapa, es decir, es a la que reducimos un globo terráqueo generador. Se indica en un mapa en forma de texto o una barra de escala. Esta escala es cierta solo en puntos seleccionados o a lo largo de líneas específicas, es decir, puntos o líneas de tangencia. La relación entre la escala real y la escala principal se describe como la relación entre la escala de mapa verdadera y la escala de mapa establecida en una ubicación particular y se denomina factor de escala (SF):
\[SF = \frac{escala\ real}{escala\ principal}\]
\(SF = 1\) para una línea de escala verdadera (también llamada unidad); \(SF > 1\) la escala real es mayor que la escala principal; \(SF < 1\) la escala real es más pequeña que la escala principal.
Por ejemplo, \(SF = 1.15\) en un mapa regional significa que la escala real es un \(15\%\) mayor que la escala principal. \(SF = 2\) significa que la distancia es dos veces mayor, mientras que \(SF = 0.5\) significa que la distancia es la mitad de la distancia real.
La distorsión de escala está relacionada con el tamaño del área de mapeo: cuanto menor sea el área por mapear, menor será la distorsión de escala. Siguiendo esta regla general, para los mapas a escala continental SF solo debe variar ligeramente de 1.0. La elección de un factor de escala influye (indirectamente) en la distancia entre las líneas secantes. Un valor comúnmente utilizado \(SF = 0.9996\), por ejemplo, da como resultado líneas secantes a una distancia de aproximadamente 360 km (180 km a cada lado desde un meridiano central). De esta manera podemos equilibrar la distorsión en el área de interés. ¡Recuerde el vídeo naranja de la Figura 4.19!
4.3 Propiedades de las Proyecciones
Al escoger la proyección del mapa, debemos considerar el objetivo que deseamos obtener. Las diferentes proyecciones tienen sus propias propiedades específicas, y cada propiedad no es exclusiva, puede ser común en algunas de ellas. Además de la elección de la proyección deberemos conocer los parámetros de la proyección cartográfica. Cada proyección tiene al menos un parámetro que controla cómo se transforman las coordenadas geográficas a coordenadas planas. Algunas proyecciones son fijas, y aparte del vector de la orientación y del factor de escala nominal, no hay otros parámetros que el usuario pueda modificar, ya que al hacerlo destruiría la definición de la proyección. En general, las proyecciones tienen parámetros severos que no pueden ser modificados.
Proyecciones diferentes causan tipos diferentes de distorsiones. Algunas proyecciones son diseñadas para reducir al mínimo la distorsión de una o dos de las características de los datos. Una proyección podría mantener el área de un elemento, pero cambiar su forma. En la Figura 4.20, los datos próximos a los laterales son estirados, los rasgos tridimensionales son comprimidos para caber en una superficie plana.
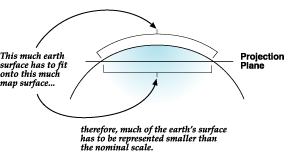
Las proyecciones de mapa son diseñadas con objetivos específicos. Una proyección de mapa podría ser usada para datos en gran escala en un área limitada, mientras otra sería usada para un mapa en pequeña escala del mundo. Las distorsiones son inevitables cuando creamos mapas planos. Los elementos del mundo tienen una posición encorvada, siguiendo la superficie esférica de la superficie terrestre. Por ello, al representarlo en un mapa, algunas porciones deberán ser estiradas o comprimidas, para encajar en el espacio.
…dependiendo de las propiedades de la proyección, la distorsión será de área, de tamaño, de distancia, de dirección o escala. No existe una proyección que no conlleve distorsión, pero cada tipo de proyección contiene solamente algún tipo de distorsión. El cartógrafo o editor de mapas debe seleccionar una proyección en que se minimice la distorsión con relación al tema o al objetivo del mapa, la cantidad de territorio, o la porción de superficie terrestre representada en el mapa.
Si bien ninguna proyección puede preservar todas las propiedades geométricas, la elección de una proyección adecuada se realiza de acuerdo con la importancia de ciertos criterios en un área/proyecto/aplicación. Hay que hacer concesiones entre las propiedades de conservación. Esto se vuelve más importante con el aumento de la distancia desde un punto o línea de tangencia, es decir, cuanto mayor es el tamaño del área de mapeo.
Las proyecciones de mapas pueden tener las siguientes propiedades geométricas:
Conforme: conserva los ángulos localmente. Un ángulo local específico en un mapa es consistente con el ángulo local respectivo en la superficie de la Tierra. Esta propiedadse refiere a la preservación local (!) de las formas (es decir, la forma correcta de una forma).
Equidistante - conserva las distancias. Una distancia medida en un mapa y multiplicada por el factor de escala da como resultado la verdadera distancia en la naturaleza. Por lo general, esta propiedad se conserva solo a lo largo de líneas tangentes o secantes o en una dirección específica.
Área equivalente: conserva el tamaño de una región. Una medida del tamaño de una región (área) en un mapa corresponde al tamaño de esa región en la realidad considerando la escala respectiva.
Dirección verdadera: conserva las direcciones globales. Una dirección específica en un mapa en cualquier punto debe corresponder a la dirección real en la que se encuentra el punto.
4.3.1 Proyecciones Conformes
Una proyección conforme preserva los ángulos y al mismo tiempo preserva localmente la forma; el término conforme significa “forma o forma correcta” (Kimerling et al. 2016). Aunque la escala varía en una proyección conforme, las distorsiones de distancia en cualquier punto son iguales en todas las direcciones. Las proyecciones conformes son particularmente importantes en el campo de la navegación, ya que representan las líneas de rumbo como las líneas rectas. (Las líneas de rumbo son segmentos de línea recta que conservan los ángulos con los meridianos.)
Con un mapa conforme, no se puede determinar la dirección en la que se encuentra un determinado punto; pero podemos determinar el azimut de este punto que nos llevará a ese punto (revisa el Problema de la Brújula). Como ya se sabe de la lección sobre sistemas de coordenadas, la distancia recorrida rara vez corresponde al camino más corto. Este último corre a lo largo de un gran círculo y requiere una corrección constante de la dirección.
4.3.1.1 Proyección de Mercator
El cartógrafo flamenco Gerhard Kremer (Figura 4.21) publicó un atlas en 1569 bajo su nombre latinizado Gerardus Mercator.

La proyección de Mercator es una proyección cilíndrica conforme que proporcionó una facilidad considerable en la navegación para generaciones de marineros durante años y sigue siendo una de las proyecciones más importantes. La proyección de Mercator en su posición normal representa casi toda la Tierra. Las áreas de las latitudes de 80° - 85 ° generalmente ya no se mapean porque la distorsión aumenta mucho en la dirección de los polos, y estos se encuentran en el infinito. La exageración del área en Europa, Rusia y América del Norte proporciona una impresión incorrecta del tamaño de las respectivas masas de tierra: explore este fenómeno en el enlace de la Figura 4.22. Por lo tanto, la utilidad de la proyección de Mercator se limita a las zonas no polares.
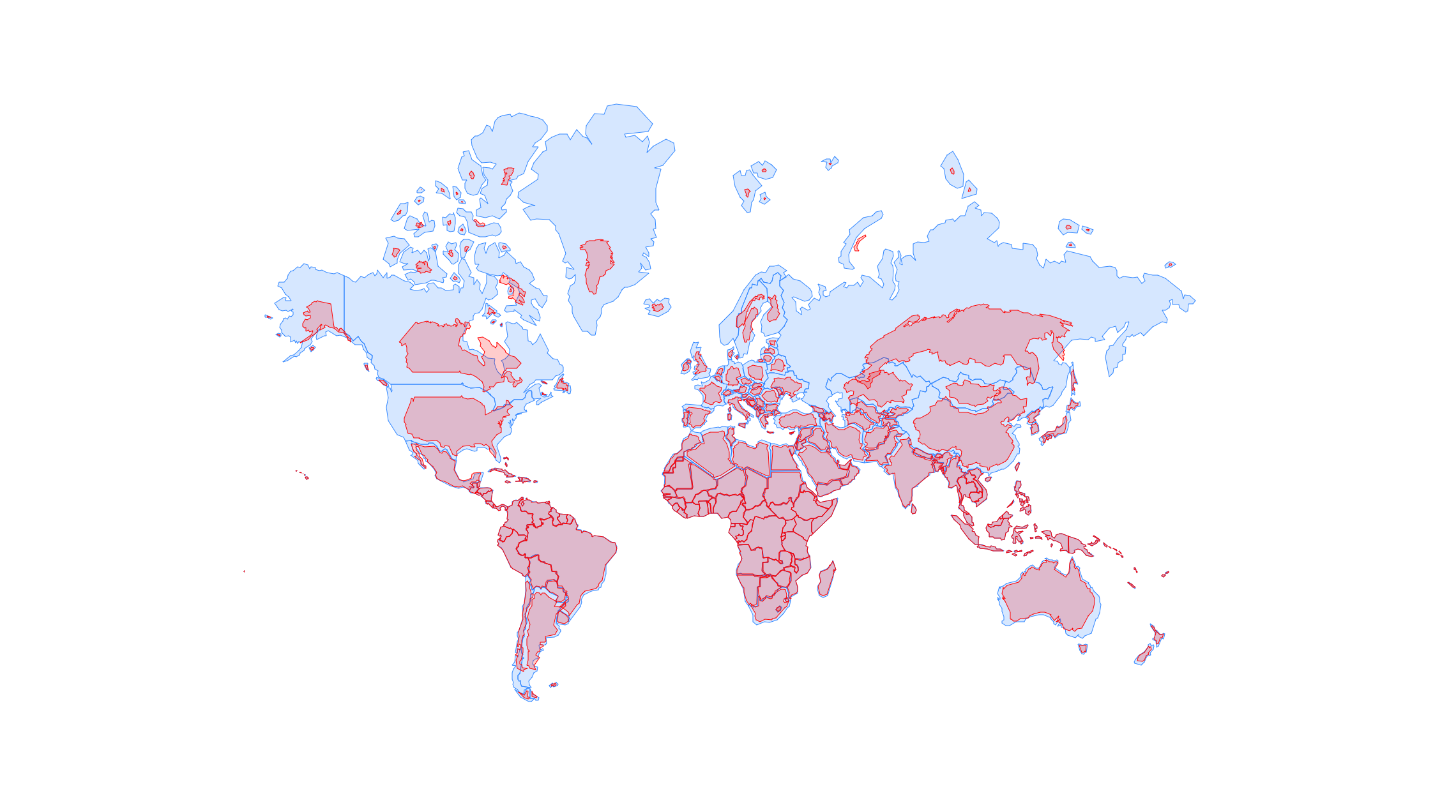
La Figura 4.23 demuestra muy bien que la proyección de Mercator es absolutamente inadecuada para mapas de toda la Tierra, debido a sus distorsiones extremas cerca de los polos. Para superar este problema, hoy en día se utiliza la proyección transversal de Mercator. A diferencia de la proyección estándar de Mercator, que se envuelve alrededor del ecuador, la proyección transversal de Mercator se gira 90° y se envuelve alrededor de un meridiano, como se puede ver en la Figura 4.23.
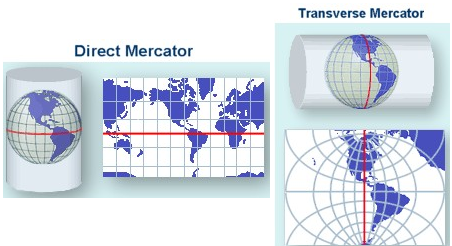
El uso más destacado de la proyección transversal de Mercator es el sistema Universal Transversal de Mercator (UTM). UTM divide la Tierra en 60 zonas, cada una de las cuales tiene 6° de ancho. Otros ejemplos de proyecciones transversales de Mercator son los sistemas cartográficos nacionales de Austria (ÖK 1:50.000) y Alemania (TK 1:25.000).
4.3.2 Proyecciones equidistantes
“Si desea determinar la distancia entre dos puntos, tome el mapa, mida la distancia entre estos puntos usando una regla y multiplique el resultado con el factor de escala del mapa …” Eso es lo que la mayoría de nosotros aprendimos en las lecciones de geografía. En muchos casos esta tarea no es tan fácil.
Observe el siguiente acertijo en la Figura 4.24: La distancia entre los puntos A y C y entre C y D es de aproximadamente 10,000 kilómetros respectivamente. ¿Cuál es la distancia entre A y D?
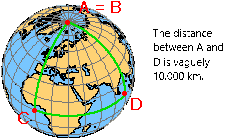
En general, es imposible crear un mapa que tenga distancias reales a escala en todas las direcciones y entre todos los puntos. Por lo tanto, hablamos de proyecciones parcialmente equidistantes.
4.3.2.1 Proyección equidistante azimutal
A diferencia de otras proyecciones equidistantes donde la “distancia verdadera” está restringida a ciertas direcciones (equidistante azimutal), en una proyección equidistante azimutal las distancias verdaderas (= esféricas) se pueden determinar en todas las direcciones. Esto, sin embargo, se aplica a un solo punto, es decir, el punto tangente. Por esta razón, esta proyección debe adaptarse específicamente a cada punto desde el que se quieran medir las distancias esféricas.
La proyección que se muestra en las Figura 4.25 es aproximadamente la proyección equidistante de Salzburgo (punto rojo aproximadamente en el medio). Las proyecciones azimutales equidistantes pueden representar no solo en un hemisferio (Figura 4.25 (a)), sino en el mundo entero (Figura 4.25 (b)). Sin embargo, las distorsiones relacionadas con la forma aumentan rápidamente hacia los bordes. Los intervalos de latitud constantes dejan claro que la longitud de los meridianos en esta situación sigue siendo la misma.
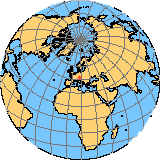
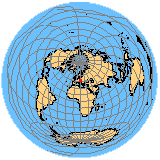
Además de la propiedad equidistante, esta proyección también conserva la dirección, pero solo en su origen, es decir, el punto de tangencia; por lo tanto, es posible determinar la dirección cardinal en la que se encuentra un punto en comparación con el origen. Debido a esta propiedad, todos los grandes círculos que pasan por el origen están representados por la proyección como líneas rectas. La propiedad de la dirección verdadera es particularmente importante para fines de navegación. Por lo tanto, refiriéndose a las cifras a continuación, no solo puede averiguar qué tan lejos está la ruta de vuelo (directa) entre Salzburgo y cualquier otro lugar, sino también sobre las áreas / lugares que se encuentran en la ruta de vuelo. Esta proyección se utiliza en una amplia gama de aplicaciones como la navegación, el relé de radio y también en la representación de regiones polares.
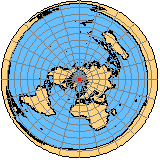
Un ejemplo popular para las proyecciones equidistantes azimutales es el logotipo de las Naciones Unidas que se muestra en la Figura 4.26:
“El logotipo de las Naciones Unidas es un mapa del mundo que representa una proyección equidistante azimutal centrada en el Polo Norte, con costillas en una corona que consiste en ramas convencionales cruzadas del olivo,… La proyección del mapa se extiende a 60 grados al sur de la latitud, e incluye cinco círculos concéntricos”.

4.3.2.2 Proyección equidistante cilíndrica
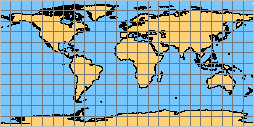
La proyección cilíndrica equidistante (equidistante cilíndrica, equilíndrica equirectangular, carta plana) solo tiene una distancia verdadera a lo largo del ecuador y los meridianos (figura a continuación). Para mediciones de distancia con una componente este u oeste, la escala aumenta rápidamente cuando se mueve desde el ecuador hacia los polos. La desviación máxima en distancias horizontales se puede ver en los polos, que se muestran en el mapa como líneas con la longitud del ecuador. Una proyección cilíndrica equidistante con la línea de tangencia en el ecuador y con el origen en 0.0 también se llama “Plate Carree” (Figura 4.27). Los grados de latitud y longitud se presentan como si fueran coordenadas cartesianas. Esta simple representación plana de coordenadas esféricas se utiliza en la mayoría de los GISystems como representación estándar de datos espaciales no proyectados.
4.3.3 Digresión: el problema de la brújula
Considere lo siguiente:
Un cohete que se lanza desde Salzburgo, Austria, se dirige hacia el este y necesita volar en línea recta alrededor del mundo.
Antes de continuar leyendo, ¿piensa en los países que cruzaría en su trayectoria de vuelo? Si pensabas que el cohete sobrevuela China y Estados Unidos, estás equivocado. En realidad, el rocket cruza el ecuador cerca de Sumatra, vuela sobre Australia, ingresa al hemisferio norte cerca de Colombia y finalmente regresa a Salzburgo. En cada punto de este camino, el cohete está exactamente al este (u oeste) del punto de partida (Salzburgo, Austria). Esto se debe a que la verdadera dirección este se determina siguiendo el gran círculo que cruza el meridiano de referencia en ángulo recto. Ahora, una situación completamente diferente surge si el cohete usa una brújula para encontrar el este y se dirige en la dirección que la brújula le indica. La trayectoria de vuelo utilizando una brújula se parecerá a un círculo de latitud / paralelo que cruza China y los Estados Unidos. Aunque el cohete ahora está volando hacia el este, ya no se refiere a su punto de partida (Austria). En cambio, utiliza el último meridiano sobre el que voló como referencia para encontrar qué dirección es hacia el este. Desde Austria, parecería que el cohete cambia constantemente su dirección de acuerdo con la dirección señalada por la brújula. Por lo tanto, una antena direccional conectada al cohete tendrá que ser ajustada / alineada continuamente.
En el caso 1, el cohete vuela a lo largo de un gran círculo y en el caso 2, se mueve a lo largo de una línea de rumbo (consulte la Lección sobre Lección 3.5 para refrescar su memoria acerca de una línea de rumbo). En el caso 1, la dirección cardinal en la que se encuentra el cohete hasta el punto de partida es constante. El ángulo (curso) cambia constantemente, pero con respecto al norte.
La situación es exactamente la contraria en el caso 2: el rumbo cambia continuamente en la dirección del movimiento dirigiéndose siempre ligeramente hacia la izquierda y, por tanto, la dirección cardinal en la que se ubica también cambia con respecto al punto de partida. Sin embargo, el ángulo respectivo (curso) - ángulo entre la última referencia cruzada y la dirección este apuntada por la brújula - con respecto al norte permanece constante.
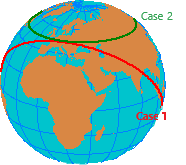
En la Figura 4.28 se puede ver que hay una diferencia significativa entre la supuesta dirección cardinal en la que se encuentra un punto de destino y la dirección cardinal que debe conservarse para llegar a ese punto. En la práctica, el tipo de aplicación determina cuál de los dos casos es necesario. Por ejemplo, la verdadera dirección es importante en el campo de la transmisión de ondas de radio o para algunas aplicaciones militares como misiles no guiados de largo alcance. El segundo caso es necesario para navegar con una brújula de A a B.
Como consecuencia, el diseño de una cuadrícula diferirá respectivamente para cumplir con varios requisitos: para determinar la dirección cardinal en la que se encuentra un punto en particular, se necesita una proyección que tenga una dirección verdadera (es decir, que sea cenital) y en la que los grandes círculos se proyecten a líneas rectas. Sin embargo, para determinar el ángulo del curso que se debe seguir para llegar a un destino, se necesita una proyección conforme en la que las líneas de rumbo se conviertan en líneas rectas.
4.3.4 Proyecciones de área equivalente
Las proyecciones de área igual conservan el tamaño relativo de las regiones en todo el mapa y tienen propiedad de equivalencia. Debido a las demandas de equivalencia, el factor de escala solo puede ser el mismo a lo largo de una o dos líneas o desde un máximo de dos puntos. Los factores de escala y los ángulos alrededor de todos los demás puntos se deformarán; por lo tanto, es imposible tener una proyección que sea de igual área y conforme al mismo tiempo. Esto solo es posible para el globo real del mundo. La forma, la distancia y la dirección están generalmente más distorsionadas hacia los bordes del mapa.
La propiedad equivalencia es mayormente necesaria en la representación a escala media y local. La propiedad de igual área siempre es importante cuando se compara un área o densidad entre regiones. Esto es cierto especialmente para los mapas del mundo que necesitan comunicar la distribución espacial de atributos como la densidad de población, la alfabetización, la pobreza y otras estadísticas relacionadas con el ser humano. En tales casos, la elección de una proyección inapropiada puede conducir a una interpretación completamente errónea de la situación. El hecho de que los mapas puedan “mentir” al distinguir superficies representadas a menudo ha sido aprovechado en aras de la propaganda.
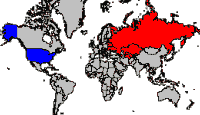
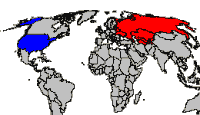
Durante la Guerra Fría, los cartógrafos estadounidenses utilizaron deliberadamente la proyección de Mercator para crear un mapa del mundo (Figura 4.29) y destacaron la URSS en rojo para que pareciera más grande, más cercana y amenazante. La Figura 4.30 muestra un mapa del mundo en la proyección de Mollweide de área igual. Nótese la diferencia en las zonas de la antigua Unión Soviética, Groenlandia y África.
4.3.4.1 Proyección azimutal de área equivalente de Lambert
Esta proyección azimutal de área equivalente (Figura 4.31) fue presentada por Johann Heinrich Lambert en 1772. Alrededor del punto de tangencia esta proyección es muy similar a la proyección equidistante azimutal discutida anteriormente. Hacia los bordes de un mapa, es decir, en las áreas del otro hemisferio, la distorsión de la distancia aumenta rápidamente para preservar los tamaños relativos de las regiones. En consecuencia, la Antártida se representa como un anillo delgado. La proyección azimutal de área equivalente de Lambert se utiliza principalmente para representar regiones pequeñas (regiones con una forma compacta).
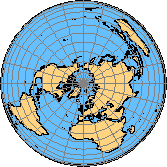
4.3.4.2 Proyección cónica de área equivalente de Albers
La construcción de la proyección cónica de área equivalente de Albers (Figura 4.32) se puede imaginar como si los rayos de luz que emanan de la superficie de la Tierra golpearan el cono de proyección en ángulo recto. Esta proyección es equidistante a lo largo de los paralelos estándar; Las distorsiones geométricas (es decir, las distorsiones de forma) que se encuentran cerca de los paralelos estándar están dentro de los límites tolerables. La proyección cónica de área equivalente de Albers es adecuada para mapas temáticos con una extensión explícita Este-Oeste, ya que la proyección comprime las áreas Norte-Sur entre cada paralelo para compensar el estiramiento Este-Oeste.
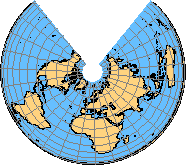
4.3.4.3 Proyección de Eckert IV
Esta proyección es similar a la proyección de Mollweide para la representación de contenido temático a escala global (Figura 4.33).
4.3.5 Proyecciones de dirección real
Las proyecciones de dirección verdadera preservan las direcciones globalmente a diferencia de las proyecciones conformes que preservan los ángulos localmente. Estas proyecciones a veces también se conocen como proyecciones azimutales porque no se puede encontrar la verdadera dirección en todas las áreas de un mapa, sino solo en el punto de tangencia (es decir, proyecciones azimutales o planas).
En los mapas azimutales, los grandes círculos que atraviesan el punto de tangencia se representan como líneas rectas. Esto nos permite determinar la dirección entre dos puntos, es decir, la forma más directa (gran segmento circular) de A a B. En la proyección gnomónica, que conserva la dirección, los grandes círculos se representan como líneas rectas que corren a través del punto de tangencia.
Si la diferencia entre la dirección verdadera y la propiedad de ángulo verdadero aún no está clara, eche un vistazo al problema de la brújula. Las proyecciones de dirección real se aplican siempre que los caminos más cortos o la propagación de línea recta sean importantes. En el pasado, las rutas de los barcos solían determinarse primero como líneas rectas en un mapa de dirección real y luego transferirse a un mapa conforme. A partir de este último mapa, se podrían leer fácilmente las correcciones necesarias que se deben realizar mientras se navega por el curso. En el campo de los relés de radio, los mapas de proyección de dirección verdadera son útiles para alinear antenas direccionales hacia ubicaciones predefinidas.
Hemos visto que existen diferentes tipos de proyecciones, todas con el mismo objetivo, representar el mundo. De todas estas proyecciones, algunas de las más utilizadas son:
- Albers Conical equal area (o área equivalente)
- Lambert Conformal Conic
- Azimuthal Equidistante
- Berhmann
- Cylindrical
- Universal Transverse Mercator (UTM)
- Mollweide
- Sinusoidal
- Eckert I
- Peters
Existe un gran número de sitios en la Internet para apreciar las diferentes proyecciones. Le invitamos a revisar los siguientes enlaces para apreciarlas. La mayoría en lengua inglesa pero técnicamente comprensible.
4.4 Visualización de las propiedades de proyección
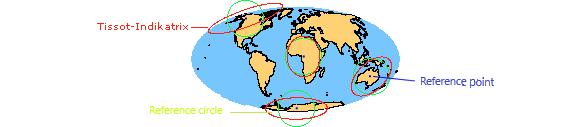
Con el fin de evaluar la naturaleza y la extensión de las distorsiones geométricas en los diseños de mapas, el matemático francés Nicolas Auguste Tissot desarrolló en el siglo 19 un indicador que determina las propiedades de una proyección en un punto: el Tissot indicatrix.
La indicatrix de Tissot muestra cómo un círculo infinitamente pequeño colocado en la superficie de la Tierra se vería proyectado en un mapa. Dado que tal círculo es demasiado pequeño para ser visible en el mapa, su forma y tamaño son muy exagerados. El tamaño y / o la forma de dicho círculo se deforma debido a la proyección. La comparación de tales círculos deformados con un círculo de referencia, el que muestra cómo se ve un círculo cuando se conservan las propiedades de proyección, indica el tipo y el grado de deformación en un punto particular del mapa.
Además, a partir de la indicatrix también podemos derivar cifras numéricas para describir y comparar cuantitativamente estas deformaciones (distorsiones). Como el grado de distorsión geométrica dentro de una proyección varía localmente, uno debe usar el indicatrix en varios puntos. Esto proporciona una buena visión general de la variación espacial de la intensidad de la deformación.
En la Figura 4.34 muestran las indicatrices de Tissot en una proyección de Mollweide. Las distorsiones de la forma se inclinan claramente hacia el borde. Dado que esta es una proyección de área igual, el área verdadera de indicatrix y el círculo de referencia coinciden en cualquier punto.
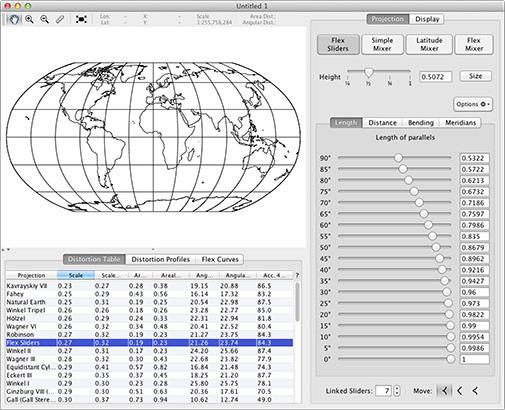
Para recrear cada una de las diferentes proyecciones vistas arriba y muchas otras más, así como desplegar las indicatrices de Tissot bajo diferentes proyecciones, le invitamos a descargar el aplicativo FlexProjector. Esta es “una aplicación de software gratuita, de código abierto y multiplataforma que permite a los cartógrafos diseñar de forma interactiva proyecciones personalizadas para mapas mundiales a pequeña escala. Se especializa en proyecciones cilíndricas y pseudocilíndricas, así como en proyecciones policónicas con paralelos curvos. Dar a los meridianos una separación no uniforme es una opción para todas las clases de proyecciones. Desde la interfaz de FlexProjector (Figura 4.35), se permite a los cartógrafos dar forma a la retícula de proyección y proporciona información visual y numérica para juzgar sus propiedades de distorsión. Los usuarios previstos de FlexProjector son aquellos sin conocimientos matemáticos especializados, incluidos los cartógrafos en ejercicio y los estudiantes de cartografía”. Una vez descargado simplemente corra el ejecutable e inicie con el comando CTRL-R y CTRL-I para visualizar más de 60 proyecciones junto con los círculos de Tissot.
4.5 Cuestionario
En el cuestionario de la Figura 4.36, haga coincidir las proyecciones del mapa con la explicación correcta. Compruebe si su solución es correcta haciendo clic en el icono de la casilla de verificación azul en la parte inferior derecha.
Finalmente, encuentre la respuesta correcta en el Cuestionario de la Figura 4.37. Compruebe si su solución es correcta haciendo clic en el icono de la casilla de verificación azul en la parte inferior derecha.
4.6 Sistemas de referencia espacial
Esta sección le dará una visión más profunda de las proyecciones actuales y los sistemas de referencia a nivel internacional, nacional y regional. Al finalizar esta lección, podrá reunir fuentes de datos heterogéneas y aplicar varias transformaciones.
4.6.1 Sistemas nacionales de referencia espacial
Los sistemas nacionales de referencia espacial se basan en elipsoides de referencia que se ajustan localmente al Geoide. Están definidos por datos de referencia locales y, por lo tanto, generalmente no son geocéntricos.
En Austria y Suiza, la topografía es llevada a cabo por las respectivas organizaciones federales (a menudo denominadas autoridad nacional de topografía) cuya tarea consiste en definir el sistema de referencia espacial preferido a nivel nacional. En Alemania, por otro lado, un sistema de referencia espacial para la topografía es responsabilidad de los estados federales individuales. Después de la reunificación alemana, se descubrió que existían varios sistemas de referencia espacial diferentes, lo que dificulta la integración de datos de diferentes fuentes.
A continuación, dos sistemas principales, Gauss-Krüger y UTM, se describen en su forma general. Luego, se ofrece una breve reseña de las posibles modificaciones de estos sistemas y otros sistemas oficiales de referencia en la región de habla alemana.
4.6.2 Sistema Gauss-Krüger
Nombrado en honor a Carl Friedrich Gauss y Louis Krüger, el sistema de referencia Gauss-Krüger se basa en una proyección transversal de Mercator que utiliza el elipsoide de Bessel como referencia para su modelo de la Tierra.
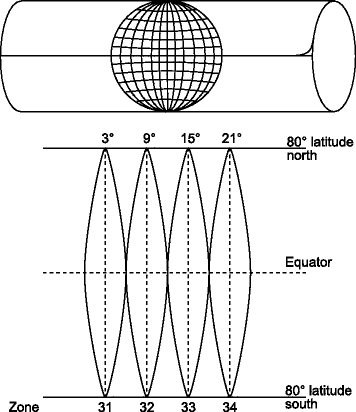
El sistema Gauss-Krüger siempre mapea zonas de 3 grados y 10 minutos (escritas como 3° 10’) de ancho de la Tierra (Figura 4.38). Dentro de dicha zona, las distorsiones geométricas son mínimas (distorsión de longitud máxima = 12 cm/km). Al girar el cilindro en pasos de 3°, se puede mapear el mundo entero en 120 zonas que se superponen cada una en 10’. Cada zona se identifica y nombra por su meridiano de referencia (meridiano central, en verde) o por su número (3 o 4), por lo que el número inicia en 0 (meridiano central = meridiano principal). El origen (0, 0) de la cuadrícula de coordenadas rectangular de Gauss-Krüger se encuentra en la intersección de cada meridiano de referencia con el ecuador.
Por lo tanto, cada zona tiene su propio sistema de coordenadas. El eje x muestra la diferencia de un punto del meridiano de referencia y se denomina este. El eje y muestra la distancia de un punto desde el ecuador y se llama norte. Ambos valores se expresan en metros. La nomenclatura x, y es ocasionalmente confusa, porque la matemática y no es igual a la geodésica x (norte). Para evitar valores negativos a la izquierda del meridiano de referencia, se añade una constante al eje x (por ejemplo, 500 km que da como resultado un falso este = 500000). Algunos estudios de sistemas nacionales, como el austriaco, “eliminan” la constante de dígitos de millón en valores grandes de un norte falso constante (por ejemplo, -5000000 m). Las coordenadas de Gauss-Krüger solo son únicas si se dispone de información adicional sobre el meridiano de referencia relevante, el número de zona y las posibles constantes (falso este / falso norte).
4.6.3 Norte verdadero vs. Norte de cuadrícula
Después de que la cuadrícula de coordenadas plana y rectangular en el sistema de Gauss-Krüger se alinea con un meridiano de referencia, la dirección norte de la cuadrícula (cuadrícula norte, en azul en la Figura 4.39) difiere del norte geográfico (en negro en la Figura 4.39) cuanto más se aleja del meridiano de referencia. El ángulo entre la cuadrícula norte y norte verdadero se llama convergencia meridiana (en verde en la Figura 4.39).
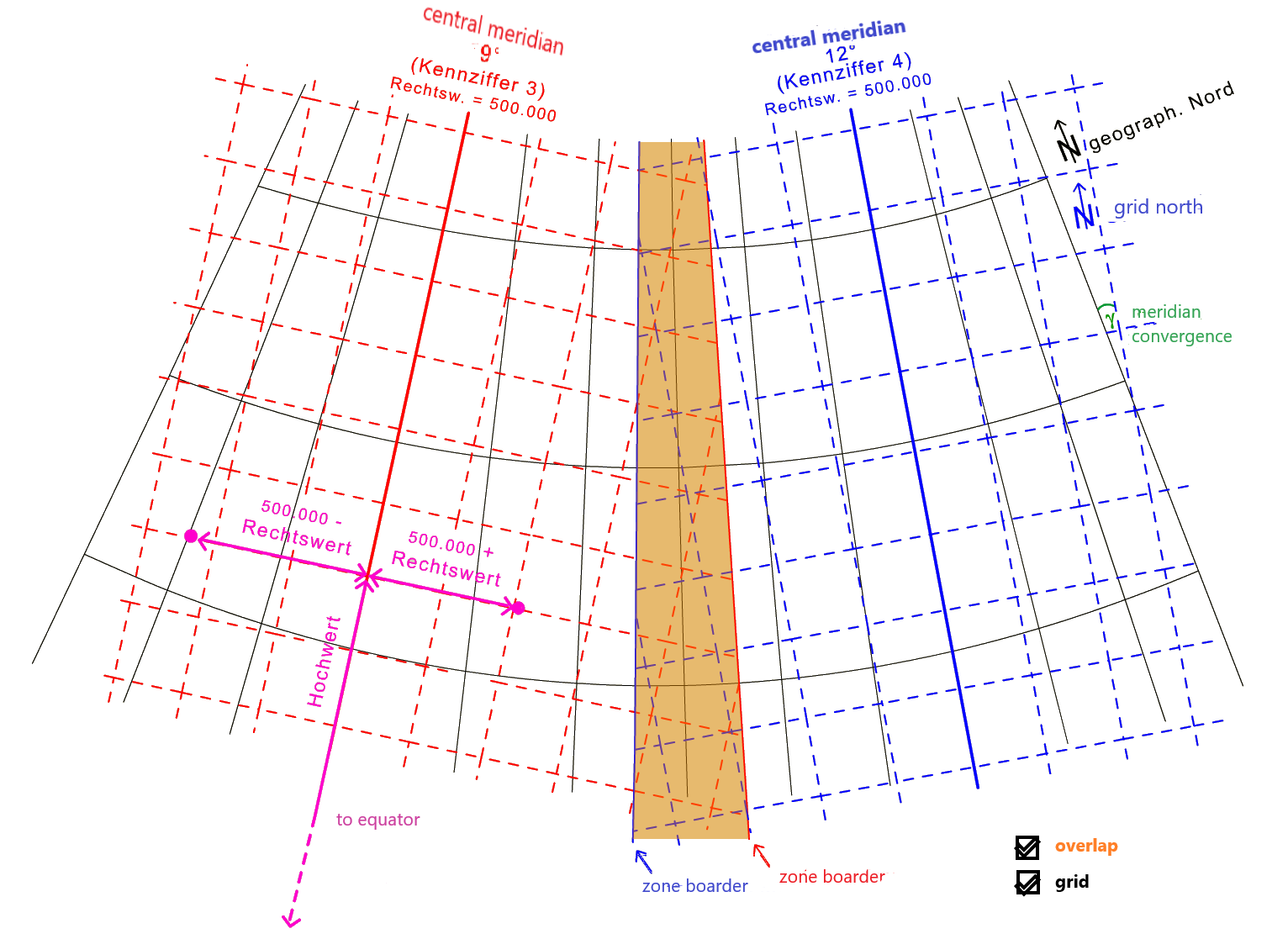
Similar situación presentaba la cartografía colombiana antes de la última resolución en la que se define un único origen nacional. Antes de 2020 el país estaba dividido en seis orígenes diferentes (Instituto Geográfico Agustín Codazzi 2020)
4.6.4 Límites de la zona`
La ventaja de la alta calidad de mapeo del sistema Gauss-Krüger tiene la desventaja de que múltiples sistemas de coordenadas localizadas no terminan sin problemas entre sí. Por ejemplo, Alemania se divide en cuatro zonas de Gauss-Krüger, con meridiano de referencia a 6 °, 9 °, 12 ° y 15 ° al este de Greenwich. Esto da como resultado “saltos de coordenadas” que ocurren durante la transición de una zona a la siguiente. Con el fin de evitar que las áreas superpuestas ubicadas en las unidades administrativas sean “cortadas” en los bordes de la zona, estas unidades a menudo se agregan a una zona que es más beneficiaria para la unidad en cuestión. Así, por ejemplo, Brandeburgo está totalmente representado en la 4ª zona, aunque partes de ella caen dentro de la 5ª zona.
4.7 UTM Universal Transversal Mercator
El sistema UTM se basa en una figura de cilindro transversal conforme. Sin embargo, a diferencia del sistema Gauss-Krüger, UTM utiliza un cilindro secante, lo que resulta en una calidad de mapeo comparable al duplicar el ancho de la zona a 6 grados (6 °) de longitud. De esta manera, toda la Tierra puede cubrirse entre 84° N y 80° S con (sólo) 60 meridianos, es decir, 60 zonas UTM. Como se muestra en la Figura 4.40, las zonas están numeradas de oeste a este, por ejemplo, la zona 1 comienza a 180 ° W y la zona 60 se extiende desde 174 ° E hasta la Línea internacional de referencia. Debido al estrecho ancho de la zona, las regiones al norte y al sur y las áreas de la capa de hielo polar se mapean en la proyección estereográfica polar universal (UPS) conforme.
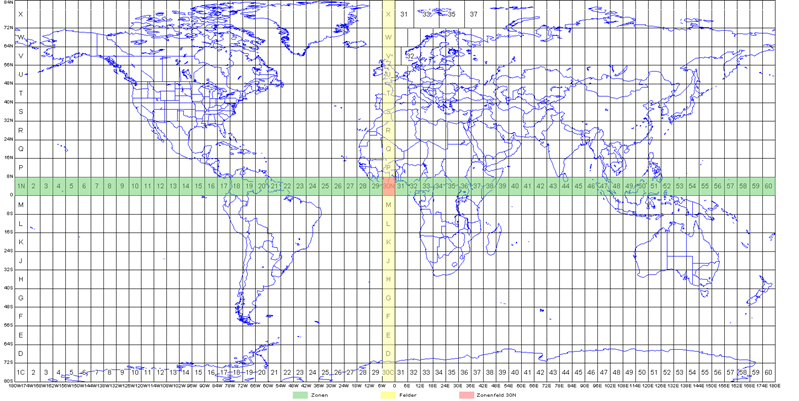
El sistema UTM fue utilizado originalmente por la OTAN durante la transición a ETRF89, pero también es utilizado por las agencias nacionales de vigilancia; por ejemplo, desde 2001, todos los mapas topográficos oficiales austriacos se convierten al sistema UTM.
Conozca la información detallada de cada zona del planeta en este sitio.
4.7.1 Parámetros de proyección UTM
Origen eje x → Meridiano Central (CM) de cada zona
- Origen eje y → Ecuador
- Unidades → Metro
- Falso Norte → Hemisferio Norte: 0m; hemisferio sur: +10000000 m
- Falso Este → +500000 metros (CM en cada zona)
- Factor de reducción en CM (cilindro secante) → 0.9996
- Datum Geodésico → Variable
4.7.2 Datum geodésico de UTM
El sistema UTM puede referirse a diferentes datum geodésicos, cada uno de los cuales es definido por autoridades nacionales o internacionales. El elipsoide Clarke 1866 (antiguo) y GRS80 (nuevo) se utilizan en los Estados Unidos. Las autoridades nacionales de topografía de la mayoría de los países europeos en la década de 1990 decidieron introducir el sistema de coordenadas UTM basado en el sistema de referencia ETRF89, que es prácticamente idéntico al GRS80 o WGS84. El elipsoide de Hayford, un (antiguo) estándar europeo de la OTAN, se usa con menos frecuencia, pero todavía se pueden encontrar algunos conjuntos de datos más antiguos que usan este datum. Por lo tanto, las coordenadas UTM son inequívocas solo cuando se proporcionan junto con el datum geodésico respectivo y la zona UTM.
4.7.3 Sistema de zonas UTM
La numeración de los meridianos comienza en la línea de fecha y va desde la zona 1 (180°W - 174°W) hasta la zona 60 (174°E - 180°E) (referir a la Figura 4.40). Para una mejor ubicación de un área dentro de una zona, cada zona UTM se divide horizontalmente en 20 bandas de latitud, donde cada banda de latitud tiene 8 grados de altura. La única excepción se puede ver en el área más remota de la Tierra, que se extiende 4 grados adicionales para terminar a 84 ° N (es decir, 72-84 ° N). Las bandas de latitud se escriben a partir de 80 ° S con la letra “C” hasta “X” en un orden alfabético. Las letras “I” y “O” se omiten porque se parece a los números 1 y 0. La intersección entre zonas y campos se denomina campo de zona.
4.7.4 Coordenadas de la cuadrícula UTM
Similar al sistema de Gauss-Krüger, el sistema UTM también construye una cuadrícula de coordenadas ortogonales en cada zona basada en el meridiano de referencia y con el origen en la intersección del meridiano de referencia y el ecuador. Para evitar problemas con las áreas en el borde de la zona, el sistema de coordenadas de cada zona supera el medio grado de ambos límites de zona (la región de superposición). Para evitar coordenadas negativas, al meridiano central de cada zona se le da un valor de este falso de 500000 metros. Para las coordenadas UTM en el hemisferio sur, se agrega un valor de norte falso de 10000000 metros. Después de la notación UTM, las coordenadas y son indicadas por “N” (Norte) y las coordenadas x por “E” (Este).
4.7.5 Determinación de zonas UTM
La zona UTM para una cierta longitud se puede encontrar utilizando un cálculo mental simple que ni siquiera requiere una ilustración.
Ejemplo 1:
Longitud de la estación base GPS en Salzburgo (13° 03’ 36.598”)
Longitud oeste = (-)° signo algebraico negativo
Longitud este = (+)13° signo algebraico positivo
Añadir 180°
Divida por 6 y redondee el resultado al entero inmediato superior.
Resultado: 13 + 180 = 193/6 = 32.166 = redondeado a la zona 33
Ejemplo 2
Longitud del centro de Manaos en Brazil (-59° 59’ 56.7024”)
Longitud oeste = (-)° signo algebraico negativo
Longitud este = (-)59° signo algebraico negativo
Añadir 180°
Divida por 6 y redondee el resultado hasta el siguiente número (el más alto).
Resultado: -59 +180 = 121/6 = 20.166 = redondeado a la zona 21
Explore el siguiente enlace dedicado a convertir coordenadas entre múltiples sistemas de coordenadas y evalúe los dos ejemplos anteriores u otros de su selección.
4.8 Sistemas alternativos
Adicionalmente a los sistemas de referencia que se refieren a longitud y latitud existen alternativas que han encontrado sus nichos. Un ejemplo bastante conocido es what3words. Aquí el mundo se rasteriza en celdas de 3x3 m y se le asigna una combinación de 3 palabras. Esta combinación de 3 palabras suele ser más fácil de recordar que las coordenadas. Tal vez quieras intentar navegar a purple.watch.vineyard o a tu propia dirección. What3Words es un sistema propietario y enlazado a un lenguaje (traducir el texto no será suficiente para que funcione).
A pesar de que esto de alguna manera parece un juego, hay esfuerzos reales realizados por el OGC y un grupo de trabajo llamado “Discrete Global Grid Systems” para aumentar la interoperabilidad internacional de datos y optimizar la potencia de procesamiento.
4.9 Lecturas adicionales:
“La promesa de sistemas de red globales discretos” sobre el grupo de trabajo OGC
4.10 Resumen
Al integrar datos espaciales de diferentes fuentes en una base de datos SIG, a menudo se espera que cumplamos una de las siguientes tareas principales (Figura 4.41):
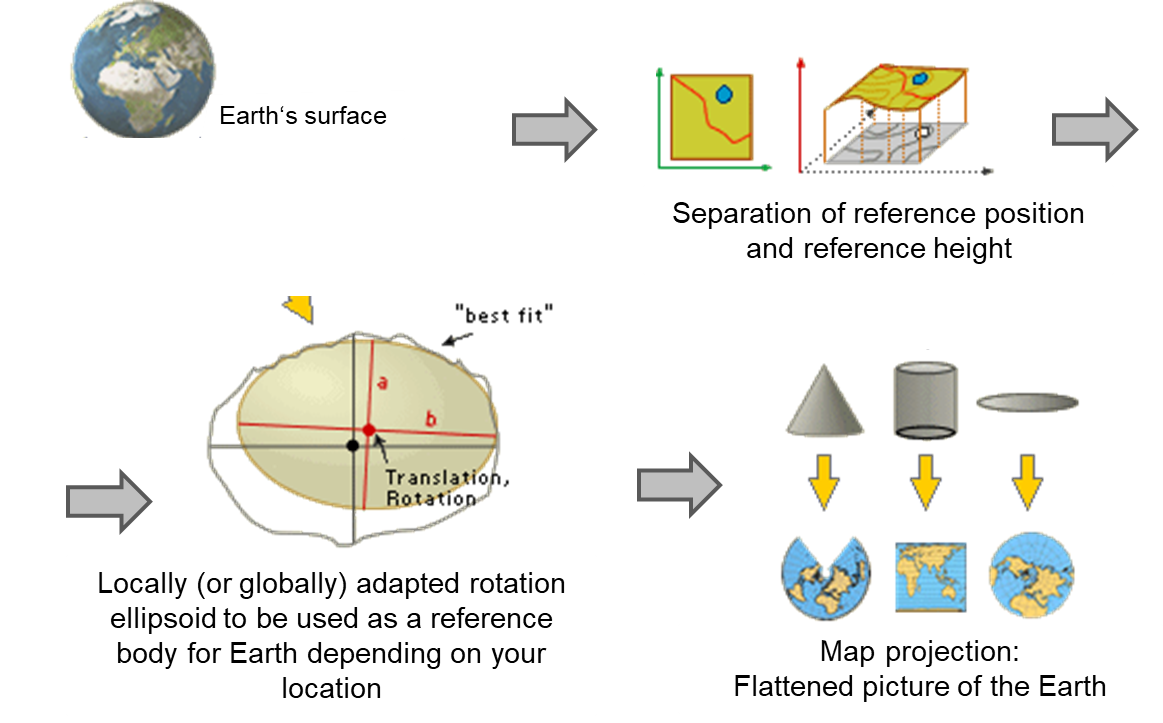
- Asigne la información de referencia y proyección correcta a un conjunto de datos.
- Cambiar una proyección de mapa conservando el datum geodésico; esto sucede, por ejemplo, al cambiar de una zona Gauss-Krüger o UTM a otra dentro del mismo sistema nacional de coordenadas.
- Cambiar la referencia geodésica de las coordenadas geográficas.
- Cambiar tanto el datum geodésico como la proyección; este caso ocurre, por ejemplo cuando deseamos integrar datos regionales (de América Latina por ejemplo) en coordenadas geográficas y en PSAD56 a coordenadas planas de un país en particular (por ejemplo Ecuador) en UTM con WGS84.
- Ajustar coordenadas locales de pantalla u hoja en un sistema de coordenadas de topografía.
Todas estas tareas se pueden llevar a cabo básicamente de dos maneras:
- Transformación de un conjunto de datos de salida en una base de datos de destino creando un resultado permanente.
- Transformación temporal y dinámica (“al vuelo”) para su visualización en la pantalla.
Finalmente, aquí hay algunos consejos para tratar con sistemas de referencia espacial en SIG:
- Compruebe a fondo los datos espaciales que reciba de fuentes desconocidas para verificar la existencia y exactitud del sistema de referencia documentado.
- Transformar/proyectar sus datos es extremadamente importante si desea utilizar su conjunto de datos para un análisis posterior (esto se aplica especialmente para datos tipo raster). Para una mera representación cartográfica es suficiente una proyección dinámica “al vuelo”.
- Compruebe siempre si se necesita una reproyección o si la tarea también requiere una transformación de referencia.
- Si su conjunto de datos no parece tener un sistema de referencia asignado, generalmente puede averiguar qué sistema de coordenadas (oficial) utiliza observando los valores de coordenadas y la ubicación del área.
Para elegir una proyección adecuada, tenga en cuenta lo siguiente:
- Sistemas de referencia existente
- Área de aplicación principal del mapa
- Tamaño del área a proyectar
- Ubicación del área en la Tierra a proyectar
- Forma del área a proyectar
En esta lección discutimos las proyecciones: la transformación geométrica de la superficie curva (elipsoidal o esférica) de la Tierra sobre una superficie plana de mapa. Analizamos varios tipos de proyecciones basadas, por ejemplo, en el desarrollo de propiedades superficiales, de aspecto o geométricas que se pueden preservar. Entender cómo funcionan las proyecciones es esencial para comprender “las relaciones internacionales en nuestra sociedad global” (Kimerling et al. 2016).
Criterios para elegir una proyección
Después de toda la discusión sobre la proyección, la elección de la adecuada ya no debería presentar un problema cercano a lo irresoluble; aquí hay algunas consideraciones que son importantes para decidir sobre la elección de una proyección apropiada:
Sistemas de referencia existentes. En muchos proyectos SIG, la cuestión de la mejor proyección a utilizar es a menudo irrelevante porque ya ha sido especificada por el cliente. Tiene mucho sentido utilizar los sistemas de referencia espacial “oficiales” o estándares como UTM en mapas a escala continental.
Área de aplicación principal del mapa. Las propiedades geométricas que se conservarán dependen del propósito de la representación real del mapa:
- La distribución o diseminación de un fenómeno se presenta preferentemente en una proyección que preserve el área.
- Los mapas para fines de navegación utilizarán proyecciones conformes, de igual área y/o equidistantes.
- Los mapas generales a escala media utilizan principalmente proyecciones que preservan el ángulo.
- Las pseudo proyecciones son las más adecuadas para los mapas del mundo que se espera que proporcionen una representación realista de la Tierra en su conjunto.
Tamaño del área a proyectar. Las diferencias entre las diversas proyecciones de mapas se hacen cada vez más obvias cuanto más nos alejamos de un punto o línea de tangencia. Por lo tanto, la decisión de una proyección en particular es más crítica si se va a cubrir un área más extensa.
Ubicación de la zona a proyectar. Principalmente para mapas de mediana y pequeña escala, la siguiente regla general resulta de cómo la superficie de proyección se ajusta al cuerpo de la Tierra:
- Proyecciones azimutales para regiones polares
- Proyecciones cónicas para proyectar regiones cercanas a los grados medios de latitud
- Proyecciones cilíndricas para áreas ecuatoriales
Forma del área a proyectar. La forma del área a proyectar solo es significativa en mapas de mediana y pequeña escala:
- Proyectos azimutales para formas más compactas
- Proyecciones cónicas o cilíndricas en áreas con una gran extensión este-oeste
- Proyecciones cilíndricas transversales en áreas estrechas con una gran extensión norte-sur
